《2025年通城学典课时作业本八年级数学下册苏科版江苏专版》

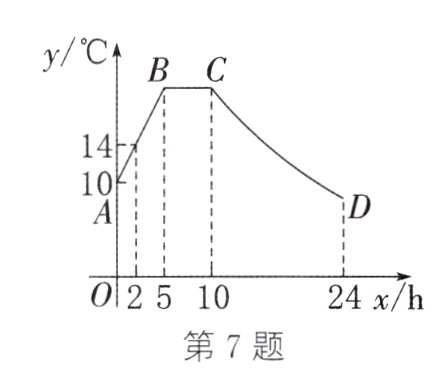
7. 某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培一种新品种蔬菜。如图所示为试验阶段的某天恒温系统从开启到关闭后，大棚内的温度$y(^{\circ}C)$与时间$x(\text{h})$之间的函数关系，其中线段$AB$、$BC$表示恒温系统开启阶段，双曲线的一部分$CD$表示恒温系统关闭阶段。请根据图中信息，解答下列问题：
（1）求这天大棚内的温度$y(^{\circ}C)$与时间$x(\text{h})$（$0 \leq x \leq 24$）之间的函数表达式；
（2）恒温系统设定的恒定温度为_______$^{\circ}C$；
（3）当大棚内的温度低于10 $^{\circ}C$时，蔬菜会受到伤害，则恒温系统最多可以关闭多少小时，才能避免蔬菜受到伤害？

答案：
(1) 设$AB$所在直线对应的函数表达式为$y = k_1x + b(k_1\neq0)$. $\because$ $AB$过点(0,10)、(2,14)，$\therefore$ $\begin{cases}b = 10\\2k_1 + b = 14\end{cases}$，解得$\begin{cases}k_1 = 2\\b = 10\end{cases}$，$\therefore$ $AB$所在直线对应的函数表达式为$y = 2x + 10$. $\because$ 点$B$在$AB$上，当$x = 5$时，$y = 2\times5 + 10 = 20$，$\therefore$ 点$B$的坐标为(5,20). $\therefore$ $BC$所在直线对应的函数表达式为$y = 20$. $\therefore$ 点$C$的坐标为(10,20). 设$CD$所在双曲线对应的函数表达式为$y=\frac{k_2}{x}(k_2\neq0)$. 将(10,20)代入，得$k_2 = 200$. $\therefore$ $CD$所在双曲线对应的函数表达式为$y=\frac{200}{x}$. 综上所述，这天大棚内的温度$y(^{\circ}C)$与时间$x$(h) ($0\leq x\leq24$) 之间的函数表达式为$y=\begin{cases}2x + 10(0\leq x＜5)\\20(5\leq x＜10)\\\frac{200}{x}(10\leq x\leq24)\end{cases}$
(2) 20
(3) 在$y=\frac{200}{x}$中，令$y = 10$，得$x = 20$，此时20 - 10 = 10(h). $\therefore$ 恒温系统最多可以关闭10 h，才能避免蔬菜受到伤害

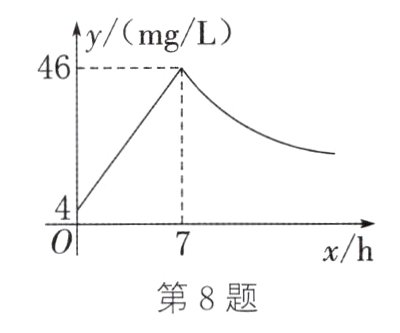
8. 在一次煤矿安全事故的调查中发现：如图，从0 h起，井内空气中$CO$（一氧化碳）的浓度达到4 mg/L，此后浓度直线上升，在7 h时达到最高，当浓度达到46 mg/L时，发生爆炸，爆炸后空气中$CO$的浓度下降，此时浓度与时间成反比例。根据题中相关信息，回答下列问题：
（1）求爆炸前、后空气中$CO$的浓度$y(\text{mg/L})$与时间$x(\text{h})$之间的函数表达式，并写出相应的自变量$x$的取值范围。
（2）当空气中的$CO$浓度达到34 mg/L时，井下3 km处的矿工接到自动报警信号，这时他们至少要以多少的速度撤离才能在爆炸前逃生？
（3）矿工只有在空气中$CO$的浓度降到4 mg/L及以下时，才能回到矿井开展生产救援工作，则矿工至少在爆炸后多长时间才能下井？

答案：
(1) 设爆炸前空气中$CO$的浓度$y$(mg/L)与时间$x$(h)之间的函数表达式为$y = k_1x + b(k_1\neq0)$. 由题图，可知直线$y = k_1x + b$过点(0,4)、(7,46)，$\therefore$ $\begin{cases}b = 4\\7k_1 + b = 46\end{cases}$，解得$\begin{cases}k_1 = 6\\b = 4\end{cases}$，$\therefore$ $y = 6x + 4$. 此时自变量$x$的取值范围是0$\leq x\leq$7. $\because$ 爆炸后空气中$CO$的浓度下降，且浓度与时间成反比例，$\therefore$ 可设$y$与$x$之间的函数表达式为$y=\frac{k_2}{x}(k_2\neq0)$. 由题图，可知函数$y=\frac{k_2}{x}$的图像过点(7,46)，$\therefore$ $\frac{k_2}{7}=46$，解得$k_2 = 322$. $\therefore$ $y=\frac{322}{x}$. 此时自变量$x$的取值范围是$x＞7$
(2) 在$y = 6x + 4$中，令$y = 34$，得6$x + 4 = 34$，解得$x = 5$. $\therefore$ 撤离的最长时间为7 - 5 = 2(h). $\therefore$ 撤离的最慢速度为3$\div$2 = 1.5(km/h)，即他们至少要以1.5 km/h的速度撤离才能在爆炸前逃生
(3) 在$y=\frac{322}{x}$中，令$y\leq4$，解得$x\geq80.5$. $\because$ 80.5 - 7 = 73.5(h)，$\therefore$ 矿工至少在爆炸后73.5 h才能下井