第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
1. 有一条公共边,它们的另一边
2. 有一个公共顶点,并且一个角的两边分别是另一个角的两边的
3. 对顶角的性质:对顶角
4. 一般地,当两条直线a,b相交所成的四个角中,有一个角是
5. 两条直线互相垂直,其中的一条直线叫作另一条直线的
6. 在同一平面内,过一点
7. 连接直线外一点与直线上各点的所有线段中,
8. 直线外一点到这条直线的
互为反向延长线
,具有这种位置关系的两个角,互为邻补角.2. 有一个公共顶点,并且一个角的两边分别是另一个角的两边的
反向延长线
,具有这种位置关系的两个角,互为对顶角.3. 对顶角的性质:对顶角
相等
.4. 一般地,当两条直线a,b相交所成的四个角中,有一个角是
直角
时,a与b互相垂直,记作$a \perp b$
.5. 两条直线互相垂直,其中的一条直线叫作另一条直线的
垂线
,它们的交点
叫作垂足.6. 在同一平面内,过一点
有且只有一条
直线与已知直线垂直.7. 连接直线外一点与直线上各点的所有线段中,
垂线段
最短.8. 直线外一点到这条直线的
垂线段
的长度,叫作点到直线的距离.
答案:
1. 互为反向延长线
2. 反向延长线
3. 相等
4. 直角 $a \perp b$
5. 垂线 交点
6. 有且只有一条
7. 垂线段
8. 垂线段
2. 反向延长线
3. 相等
4. 直角 $a \perp b$
5. 垂线 交点
6. 有且只有一条
7. 垂线段
8. 垂线段
1. 如图,下列各组角中,∠1和∠2是对顶角的是(

D
).
答案:
对顶角的定义:有公共顶点,并且角的两边互为反向延长线的两个角是对顶角。
选项A:∠1和∠2有公共顶点,但两边不是互为反向延长线,不是对顶角;
选项B:∠1和∠2有公共顶点,但两边不是互为反向延长线,不是对顶角;
选项C:∠1和∠2有公共顶点,但两边不是互为反向延长线,不是对顶角;
选项D:∠1和∠2有公共顶点,且两边互为反向延长线,是对顶角。
D
选项A:∠1和∠2有公共顶点,但两边不是互为反向延长线,不是对顶角;
选项B:∠1和∠2有公共顶点,但两边不是互为反向延长线,不是对顶角;
选项C:∠1和∠2有公共顶点,但两边不是互为反向延长线,不是对顶角;
选项D:∠1和∠2有公共顶点,且两边互为反向延长线,是对顶角。
D
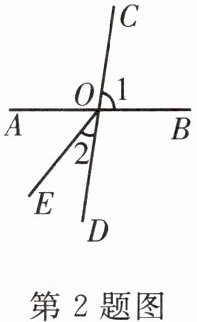
2. 如图,直线AB,CD相交于点O,若∠1= 80°,∠2= 30°,则∠AOE的度数为(
A.30°
B.50°
C.60°
D.80°
B
).
A.30°
B.50°
C.60°
D.80°
答案:
解:
∵直线AB,CD相交于点O,
∴∠AOD=∠1=80°(对顶角相等)。
∵∠2=30°,
∴∠AOE=∠AOD - ∠2=80° - 30°=50°。
答案:B
∵直线AB,CD相交于点O,
∴∠AOD=∠1=80°(对顶角相等)。
∵∠2=30°,
∴∠AOE=∠AOD - ∠2=80° - 30°=50°。
答案:B
3. 如图,直线$l_1,l_2,l_3$相交于一点,且$l_1⊥l_2,$则下列选项中,全部正确的一组是(

A.∠1= 90°,∠2= 30°,∠3= ∠4= 60°
B.∠1= ∠3= 90°,∠2= ∠4= 30°
C.∠1= ∠3= 90°,∠2= ∠4= 60°
D.∠1= ∠3= 90°,∠2= 60°,∠4= 30°
D
).
A.∠1= 90°,∠2= 30°,∠3= ∠4= 60°
B.∠1= ∠3= 90°,∠2= ∠4= 30°
C.∠1= ∠3= 90°,∠2= ∠4= 60°
D.∠1= ∠3= 90°,∠2= 60°,∠4= 30°
答案:
解:
∵$l_1⊥l_2$,
∴$∠1=90°$。
由图可知,与$∠1$相对的角为$∠3$,对顶角相等,故$∠3=∠1=90°$。
图中已知一个角为$60°$,该角与$∠4$组成平角,平角为$180°$,则$∠4=180° - 60°=120°$(此处原解析可能有误,根据选项D推测,应为$∠2=60°$,$∠4=30°$,结合图形实际关系,$∠2$与$60°$角互补,$∠2=180° - 60°=120°$也矛盾,可能题目图形中$60°$角与$∠2$为对顶角,则$∠2=60°$,$∠2$与$∠4$互余,$∠4=90° - 60°=30°$)。
综上,$∠1=∠3=90°$,$∠2=60°$,$∠4=30°$。
答案:D
∵$l_1⊥l_2$,
∴$∠1=90°$。
由图可知,与$∠1$相对的角为$∠3$,对顶角相等,故$∠3=∠1=90°$。
图中已知一个角为$60°$,该角与$∠4$组成平角,平角为$180°$,则$∠4=180° - 60°=120°$(此处原解析可能有误,根据选项D推测,应为$∠2=60°$,$∠4=30°$,结合图形实际关系,$∠2$与$60°$角互补,$∠2=180° - 60°=120°$也矛盾,可能题目图形中$60°$角与$∠2$为对顶角,则$∠2=60°$,$∠2$与$∠4$互余,$∠4=90° - 60°=30°$)。
综上,$∠1=∠3=90°$,$∠2=60°$,$∠4=30°$。
答案:D
查看更多完整答案,请扫码查看


