2025年天利38套高中名校期中期末联考测试卷高中数学必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年天利38套高中名校期中期末联考测试卷高中数学必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 集合$\{2a,a^{2}\}$中实数$a$的取值范围是(
A.$\{a|a = 0$,或$a = 2\}$
B.$\{a|a = 0$,且$a = 2\}$
C.$\{a|a\neq0$,或$a\neq2\}$
D.$\{a|a\neq0$,且$a\neq2\}$
D
)A.$\{a|a = 0$,或$a = 2\}$
B.$\{a|a = 0$,且$a = 2\}$
C.$\{a|a\neq0$,或$a\neq2\}$
D.$\{a|a\neq0$,且$a\neq2\}$
答案:
1.D集合元素的互异性 由集合元素的互异性可知,$2a \neq a^2$,解得$a \neq 0$且$a \neq 2$,所以实数$a$的取值范围为$\{a \mid a \neq 0, 且 a \neq 2\}$,故选D.
2. 下列四组函数中,表示相同函数的一组是(
A.$f(x)=\sqrt{x + 1}·\sqrt{x - 1}$,$g(x)=\sqrt{x^{2}-1}$
B.$f(x)=\sqrt{x^{2}}$,$g(x)=(\sqrt{x})^{2}$
C.$f(x)=\begin{cases}1,&x\geq0,\\ -1,&x\lt0,\end{cases}$ $g(x)=\begin{cases}\dfrac{x}{|x|},&x\neq0,\\ 1,&x = 0\end{cases}$
D.$f(x)=1$,$g(x)=x^{0}$
C
)A.$f(x)=\sqrt{x + 1}·\sqrt{x - 1}$,$g(x)=\sqrt{x^{2}-1}$
B.$f(x)=\sqrt{x^{2}}$,$g(x)=(\sqrt{x})^{2}$
C.$f(x)=\begin{cases}1,&x\geq0,\\ -1,&x\lt0,\end{cases}$ $g(x)=\begin{cases}\dfrac{x}{|x|},&x\neq0,\\ 1,&x = 0\end{cases}$
D.$f(x)=1$,$g(x)=x^{0}$
答案:
2.C 函数的定义 对于A,函数$f(x)=\sqrt{x + 1} · \sqrt{x - 1}$的定义域为$\{x \mid x \geq 1\}$,函数$g(x)=\sqrt{x^2 - 1}$的定义域为$\{x \mid x \geq 1 或 x \leq -1\}$,故两个函数的定义域不一样,不是相同函数,故A错误;对于B,函数$f(x)=\sqrt{x^2}$的定义域为$\mathbf{R}$,函数$g(x)=(\sqrt{x})^2$的定义域为$\{x \mid x \geq 0\}$,故两个函数的定义域不一样,不是相同函数,故B错误;对于C,$f(x)=\begin{cases} 1, & x \geq 0, \\ -1, & x < 0, \end{cases}$ $g(x)=\begin{cases} \frac{x}{\mid x \mid}, & x \neq 0, \\ 1, & x = 0 \end{cases} = \begin{cases} 1, & x \geq 0, \\ -1, & x < 0, \end{cases} = f(x)$,故C正确;对于D,函数$f(x)=1$的定义域为$\mathbf{R}$,函数$g(x)=x^0$的定义域为$\{x \mid x \neq 0\}$,故两个函数的定义域不一样,不是相同函数,故D错误,故选C.
3. 荀子曰:“故不积跬步,无以至千里;不积小流,无以成江海”。这句来自先秦时期的名言。此名言中的“积跬步”是“至千里”的(
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
B
)A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:
3.B充分、必要条件的判断 由名言可知“积跬步”不一定“至千里”,但要“至千里”必须“积跬步”,故“积跬步”是“至千里”的必要不充分条件,故选B.
4. 树德中学 2023 年秋季运动会亮点之一——师生火炬传递,火炬如图 1 所示,数学建模活动时将其抽象为图 2 所示的几何体。假设火炬装满燃料,燃烧时燃料以均匀的速度消耗,记剩余燃料的高度为$h$,则$h$关于时间$t$的函数的大致图象可能是(
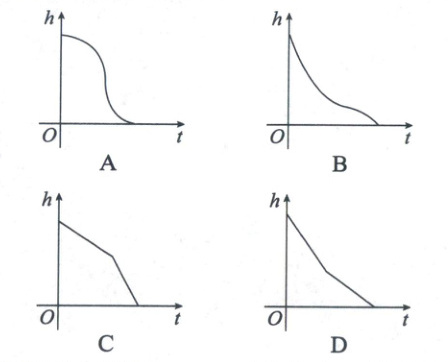
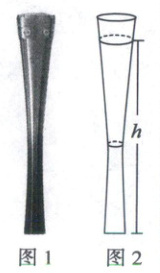
A
)

答案:
4.A 函数图象的识别 由题图可知,该火炬中间细,上下粗,燃烧时燃料以均匀的速度消耗,燃料在燃烧时,燃料的高度一直在下降,刚开始时下降的速度越来越快,在燃料到达火炬最细处后,燃料的高度下降得越来越慢,结合选项可知,A选项符合题意,故选A.
5. 满足$\{1\}\subseteq A\subsetneqq\{1,2,3,4\}$的集合$A$的个数为(
A.7
B.8
C.15
D.16
A
)A.7
B.8
C.15
D.16
答案:
5.A 集合间的基本关系
通解:$\because \{1\} \subseteq \mathrm{A}, \therefore 1 \in \mathrm{A}. \because \mathrm{A} \subseteq \{1,2,3,4\}$,$\therefore$满足题意的集合A有$\{1\},\{1,2\},\{1,3\},\{1,4\},\{1,2,3\},\{1,2,4\},\{1,3,4\}$,共7个,故选A.
快解:因为$\{1\} \subseteq \mathrm{A} \subseteq \{1,2,3,4\}$,所以$1 \in \mathrm{A}$,所以只需求出集合$\{2,3,4\}$的真子集个数即可,所以满足题意的集合A的个数为$2^3 - 1 = 7$个,故选A.
通解:$\because \{1\} \subseteq \mathrm{A}, \therefore 1 \in \mathrm{A}. \because \mathrm{A} \subseteq \{1,2,3,4\}$,$\therefore$满足题意的集合A有$\{1\},\{1,2\},\{1,3\},\{1,4\},\{1,2,3\},\{1,2,4\},\{1,3,4\}$,共7个,故选A.
快解:因为$\{1\} \subseteq \mathrm{A} \subseteq \{1,2,3,4\}$,所以$1 \in \mathrm{A}$,所以只需求出集合$\{2,3,4\}$的真子集个数即可,所以满足题意的集合A的个数为$2^3 - 1 = 7$个,故选A.
6. 已知函数$y=\dfrac{3x + 2}{x - 1}$,$x\in(m,n]$的最小值为 8,则实数$m$的取值范围是(
A.$(0,1)$
B.$(1,2)$
C.$(1,2]$
D.$[1,2)$
D
)A.$(0,1)$
B.$(1,2)$
C.$(1,2]$
D.$[1,2)$
答案:
6.D 函数的最值 因为$y = \frac{3x + 2}{x - 1} = \frac{3(x - 1) + 5}{x - 1} = 3 + \frac{5}{x - 1}$,$x \neq 1$,所以$y = 3 + \frac{5}{x - 1}$在$(m,n]$上单调递减,所以$y = 3 + \frac{5}{x - 1}$在$x = n$处取到的最小值为8,即$3 + \frac{5}{n - 1} = 8$,解得$n = 2$,所以$1 \leq m < 2$,故选D.
7. 定义在$\mathbf{R}$上的函数$y = f(x)$满足以下条件:
①函数$y = f(x + 1)$是偶函数;②对任意$x_{1}$,$x_{2}\in(-\infty,1]$,当$x_{1}\neq x_{2}$时都有$(x_{1}-x_{2})·(f(x_{2})-f(x_{1}))\gt0$,则$f(0)$,$f(\dfrac{3}{2})$,$f(-3)$的大小关系为(
A.$f(\dfrac{3}{2})\gt f(0)\gt f(-3)$
B.$f(-3)\gt f(0)\gt f(\dfrac{3}{2})$
C.$f(\dfrac{3}{2})\gt f(-3)\gt f(0)$
D.$f(-3)\gt f(\dfrac{3}{2})\gt f(0)$
①函数$y = f(x + 1)$是偶函数;②对任意$x_{1}$,$x_{2}\in(-\infty,1]$,当$x_{1}\neq x_{2}$时都有$(x_{1}-x_{2})·(f(x_{2})-f(x_{1}))\gt0$,则$f(0)$,$f(\dfrac{3}{2})$,$f(-3)$的大小关系为(
B
)A.$f(\dfrac{3}{2})\gt f(0)\gt f(-3)$
B.$f(-3)\gt f(0)\gt f(\dfrac{3}{2})$
C.$f(\dfrac{3}{2})\gt f(-3)\gt f(0)$
D.$f(-3)\gt f(\dfrac{3}{2})\gt f(0)$
答案:
7.B 利用函数的对称性和单调性比较大小
【思维导图】$y = f(x + 1)$是偶函数$\rightarrow f(x)$的图象关于直线$x = 1$对称$\rightarrow f(x)$在$(-\infty,1]$上的单调性$\rightarrow$得解.
由函数$y = f(x + 1)$是偶函数,所以函数$y = f(x)$的图象关于直线$x = 1$对称. 又对任意$x_1,x_2 \in (-\infty,1]$,当$x_1 \neq x_2$时都有$(x_1 - x_2)(f(x_2) - f(x_1)) > 0$,所以函数$y = f(x)$在$(-\infty,1]$上单调递减(题眼). 又$f(\frac{3}{2}) = f(\frac{1}{2})$,$-3 < 0 < \frac{1}{2} < 1$,所以$f(-3) > f(0) > f(\frac{1}{2})$(提示:函数单调性的应用),所以$f(-3) > f(0) > f(\frac{3}{2})$,故选B.
【思维导图】$y = f(x + 1)$是偶函数$\rightarrow f(x)$的图象关于直线$x = 1$对称$\rightarrow f(x)$在$(-\infty,1]$上的单调性$\rightarrow$得解.
由函数$y = f(x + 1)$是偶函数,所以函数$y = f(x)$的图象关于直线$x = 1$对称. 又对任意$x_1,x_2 \in (-\infty,1]$,当$x_1 \neq x_2$时都有$(x_1 - x_2)(f(x_2) - f(x_1)) > 0$,所以函数$y = f(x)$在$(-\infty,1]$上单调递减(题眼). 又$f(\frac{3}{2}) = f(\frac{1}{2})$,$-3 < 0 < \frac{1}{2} < 1$,所以$f(-3) > f(0) > f(\frac{1}{2})$(提示:函数单调性的应用),所以$f(-3) > f(0) > f(\frac{3}{2})$,故选B.
查看更多完整答案,请扫码查看


