2025年世纪金榜新视野暑假作业高一数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年世纪金榜新视野暑假作业高一数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
1. 下列物理量:①质量;②速度;③位移;④力;⑤加速度;⑥路程;⑦密度. 其中不是向量的有(
A.1个
B.2个
C.3个
D.4个
C
)A.1个
B.2个
C.3个
D.4个
答案:
解:向量是既有大小又有方向的量。
①质量只有大小,没有方向,不是向量;
②速度既有大小又有方向,是向量;
③位移既有大小又有方向,是向量;
④力既有大小又有方向,是向量;
⑤加速度既有大小又有方向,是向量;
⑥路程只有大小,没有方向,不是向量;
⑦密度只有大小,没有方向,不是向量。
不是向量的有①⑥⑦,共3个。
答案:C
①质量只有大小,没有方向,不是向量;
②速度既有大小又有方向,是向量;
③位移既有大小又有方向,是向量;
④力既有大小又有方向,是向量;
⑤加速度既有大小又有方向,是向量;
⑥路程只有大小,没有方向,不是向量;
⑦密度只有大小,没有方向,不是向量。
不是向量的有①⑥⑦,共3个。
答案:C
2. 在下列判断中,正确的是(
①长度为0的向量都是零向量;
②零向量的方向都是相同的;
③长度相等的向量都是单位向量;
④单位向量都是同方向;
⑤向量$\overrightarrow{AB}与向量\overrightarrow{BA}$的长度相等.
A.①②③
B.①③⑤
C.①②⑤
D.①⑤
D
)①长度为0的向量都是零向量;
②零向量的方向都是相同的;
③长度相等的向量都是单位向量;
④单位向量都是同方向;
⑤向量$\overrightarrow{AB}与向量\overrightarrow{BA}$的长度相等.
A.①②③
B.①③⑤
C.①②⑤
D.①⑤
答案:
【解析】:
首先,我们逐一分析每个判断:
①长度为0的向量都是零向量。这是正确的,因为零向量的定义就是长度为0的向量。
②零向量的方向都是相同的。这是错误的,因为零向量没有确定的方向,或者说其方向是任意的。
③长度相等的向量都是单位向量。这是错误的,单位向量的定义是长度为1的向量,而长度相等的向量并不一定长度都为1。
④单位向量都是同方向。这也是错误的,单位向量只要求长度为1,方向可以是任意的。
⑤向量$\overrightarrow{AB}$与向量$\overrightarrow{BA}$的长度相等。这是正确的,因为向量$\overrightarrow{AB}$与向量$\overrightarrow{BA}$是相反向量,它们的长度是相等的。
接下来,我们根据上述分析,对照选项进行判断:
A.①②③:包含错误的判断②和③,所以A错误;
B.①③⑤:包含错误的判断③,所以B错误;
C.①②⑤:包含错误的判断②,所以C错误;
D.①⑤:包含正确的判断①和⑤,所以D正确。
【答案】:D.①⑤。
首先,我们逐一分析每个判断:
①长度为0的向量都是零向量。这是正确的,因为零向量的定义就是长度为0的向量。
②零向量的方向都是相同的。这是错误的,因为零向量没有确定的方向,或者说其方向是任意的。
③长度相等的向量都是单位向量。这是错误的,单位向量的定义是长度为1的向量,而长度相等的向量并不一定长度都为1。
④单位向量都是同方向。这也是错误的,单位向量只要求长度为1,方向可以是任意的。
⑤向量$\overrightarrow{AB}$与向量$\overrightarrow{BA}$的长度相等。这是正确的,因为向量$\overrightarrow{AB}$与向量$\overrightarrow{BA}$是相反向量,它们的长度是相等的。
接下来,我们根据上述分析,对照选项进行判断:
A.①②③:包含错误的判断②和③,所以A错误;
B.①③⑤:包含错误的判断③,所以B错误;
C.①②⑤:包含错误的判断②,所以C错误;
D.①⑤:包含正确的判断①和⑤,所以D正确。
【答案】:D.①⑤。
3. 下列说法正确的是(
A.有向线段$\overrightarrow{AB}与\overrightarrow{BA}$表示同一向量
B.两个有公共终点的向量是平行向量
C.零向量与单位向量是平行向量
D.对任意向量$\boldsymbol{a}$,$\frac{\boldsymbol{a}}{\vert\boldsymbol{a}\vert}$是一个单位向量
C
)A.有向线段$\overrightarrow{AB}与\overrightarrow{BA}$表示同一向量
B.两个有公共终点的向量是平行向量
C.零向量与单位向量是平行向量
D.对任意向量$\boldsymbol{a}$,$\frac{\boldsymbol{a}}{\vert\boldsymbol{a}\vert}$是一个单位向量
答案:
【解析】:
本题主要考察平面向量的基本概念,包括向量的表示、平行向量的定义、零向量与单位向量的性质。
A选项:有向线段$\overrightarrow{AB}$与$\overrightarrow{BA}$虽然长度相同,但方向相反,因此它们不是同一向量。向量是有方向和大小的量,方向不同则向量不同。
B选项:两个有公共终点的向量,并不意味着它们是平行向量。平行向量的定义是方向相同或相反的非零向量,与起点和终点位置无关。
C选项:零向量与任意向量都平行,包括单位向量。因为零向量没有方向,可以认为它与任意方向都平行。
D选项:对于任意向量$\boldsymbol{a}$,$\frac{\boldsymbol{a}}{\vert\boldsymbol{a}\vert}$是将$\boldsymbol{a}$单位化,即得到一个与$\boldsymbol{a}$方向相同但模长为1的向量。但是,当$\boldsymbol{a} = \boldsymbol{0}$(零向量)时,$\vert\boldsymbol{a}\vert = 0$,此时$\frac{\boldsymbol{a}}{\vert\boldsymbol{a}\vert}$无意义。因此,D选项的描述不完全准确。
【答案】:
C
本题主要考察平面向量的基本概念,包括向量的表示、平行向量的定义、零向量与单位向量的性质。
A选项:有向线段$\overrightarrow{AB}$与$\overrightarrow{BA}$虽然长度相同,但方向相反,因此它们不是同一向量。向量是有方向和大小的量,方向不同则向量不同。
B选项:两个有公共终点的向量,并不意味着它们是平行向量。平行向量的定义是方向相同或相反的非零向量,与起点和终点位置无关。
C选项:零向量与任意向量都平行,包括单位向量。因为零向量没有方向,可以认为它与任意方向都平行。
D选项:对于任意向量$\boldsymbol{a}$,$\frac{\boldsymbol{a}}{\vert\boldsymbol{a}\vert}$是将$\boldsymbol{a}$单位化,即得到一个与$\boldsymbol{a}$方向相同但模长为1的向量。但是,当$\boldsymbol{a} = \boldsymbol{0}$(零向量)时,$\vert\boldsymbol{a}\vert = 0$,此时$\frac{\boldsymbol{a}}{\vert\boldsymbol{a}\vert}$无意义。因此,D选项的描述不完全准确。
【答案】:
C
4. 如图,梯形$ABCD$为等腰梯形,则两腰上的向量$\overrightarrow{AB}与\overrightarrow{DC}$的关系是(
A.$\overrightarrow{AB}= \overrightarrow{DC}$
B.$\vert\overrightarrow{AB}\vert=\vert\overrightarrow{DC}\vert$
C.$\overrightarrow{AB}>\overrightarrow{DC}$
D.$\overrightarrow{AB}<\overrightarrow{DC}$
B
)A.$\overrightarrow{AB}= \overrightarrow{DC}$
B.$\vert\overrightarrow{AB}\vert=\vert\overrightarrow{DC}\vert$
C.$\overrightarrow{AB}>\overrightarrow{DC}$
D.$\overrightarrow{AB}<\overrightarrow{DC}$
答案:
解:由4题图可知,等腰梯形ABCD中,AB和CD为两腰。
等腰梯形两腰长度相等,即线段AB与DC长度相等。
向量的模表示向量的长度,所以$|\overrightarrow{AB}| = |\overrightarrow{DC}|$。
向量相等需大小相等且方向相同,$\overrightarrow{AB}$与$\overrightarrow{DC}$方向不同,故$\overrightarrow{AB} \neq \overrightarrow{DC}$。
向量不能比较大小,C、D选项错误。
答案:B
等腰梯形两腰长度相等,即线段AB与DC长度相等。
向量的模表示向量的长度,所以$|\overrightarrow{AB}| = |\overrightarrow{DC}|$。
向量相等需大小相等且方向相同,$\overrightarrow{AB}$与$\overrightarrow{DC}$方向不同,故$\overrightarrow{AB} \neq \overrightarrow{DC}$。
向量不能比较大小,C、D选项错误。
答案:B
5. 下列命题正确的是(
A.向量$\boldsymbol{a}与\boldsymbol{b}$共线,向量$\boldsymbol{b}与\boldsymbol{c}$共线,则向量$\boldsymbol{a}与\boldsymbol{c}$共线
B.向量$\boldsymbol{a}与\boldsymbol{b}$不共线,向量$\boldsymbol{b}与\boldsymbol{c}$不共线,则向量$\boldsymbol{a}与\boldsymbol{c}$不共线
C.向量$\overrightarrow{AB}与\overrightarrow{CD}$是共线向量,则$A$,$B$,$C$,$D$四点一定共线
D.向量$\boldsymbol{a}与\boldsymbol{b}$不共线,则$\boldsymbol{a}与\boldsymbol{b}$都是非零向量
D
)A.向量$\boldsymbol{a}与\boldsymbol{b}$共线,向量$\boldsymbol{b}与\boldsymbol{c}$共线,则向量$\boldsymbol{a}与\boldsymbol{c}$共线
B.向量$\boldsymbol{a}与\boldsymbol{b}$不共线,向量$\boldsymbol{b}与\boldsymbol{c}$不共线,则向量$\boldsymbol{a}与\boldsymbol{c}$不共线
C.向量$\overrightarrow{AB}与\overrightarrow{CD}$是共线向量,则$A$,$B$,$C$,$D$四点一定共线
D.向量$\boldsymbol{a}与\boldsymbol{b}$不共线,则$\boldsymbol{a}与\boldsymbol{b}$都是非零向量
答案:
【解析】:
本题主要考察平面向量的基本概念以及向量共线的性质。
A选项:若向量$\boldsymbol{b}$是零向量,那么它与任意向量都共线。即使$\boldsymbol{a}$与$\boldsymbol{b}$共线,$\boldsymbol{b}$与$\boldsymbol{c}$共线,也不能保证$\boldsymbol{a}$与$\boldsymbol{c}$共线,因为$\boldsymbol{b}$可能是零向量。所以A选项错误。
B选项:即使$\boldsymbol{a}$与$\boldsymbol{b}$不共线,$\boldsymbol{b}$与$\boldsymbol{c}$不共线,也不能直接推断出$\boldsymbol{a}$与$\boldsymbol{c}$不共线。例如,$\boldsymbol{a}$和$\boldsymbol{c}$可能共线,但与$\boldsymbol{b}$都不共线。所以B选项错误。
C选项:即使向量$\overrightarrow{AB}$与$\overrightarrow{CD}$是共线向量,这并不意味着$A$,$B$,$C$,$D$四点一定共线。例如,$A$,$B$,$C$,$D$可能构成一个平行四边形,其中$\overrightarrow{AB}$与$\overrightarrow{CD}$共线,但四点不共线。所以C选项错误。
D选项:如果两个向量不共线,那么它们都不能是零向量。因为零向量与任意向量都共线,所以如果其中一个向量是零向量,那么它们就会共线。因此,如果$\boldsymbol{a}$与$\boldsymbol{b}$不共线,那么它们都必须是非零向量。所以D选项正确。
【答案】:
D
本题主要考察平面向量的基本概念以及向量共线的性质。
A选项:若向量$\boldsymbol{b}$是零向量,那么它与任意向量都共线。即使$\boldsymbol{a}$与$\boldsymbol{b}$共线,$\boldsymbol{b}$与$\boldsymbol{c}$共线,也不能保证$\boldsymbol{a}$与$\boldsymbol{c}$共线,因为$\boldsymbol{b}$可能是零向量。所以A选项错误。
B选项:即使$\boldsymbol{a}$与$\boldsymbol{b}$不共线,$\boldsymbol{b}$与$\boldsymbol{c}$不共线,也不能直接推断出$\boldsymbol{a}$与$\boldsymbol{c}$不共线。例如,$\boldsymbol{a}$和$\boldsymbol{c}$可能共线,但与$\boldsymbol{b}$都不共线。所以B选项错误。
C选项:即使向量$\overrightarrow{AB}$与$\overrightarrow{CD}$是共线向量,这并不意味着$A$,$B$,$C$,$D$四点一定共线。例如,$A$,$B$,$C$,$D$可能构成一个平行四边形,其中$\overrightarrow{AB}$与$\overrightarrow{CD}$共线,但四点不共线。所以C选项错误。
D选项:如果两个向量不共线,那么它们都不能是零向量。因为零向量与任意向量都共线,所以如果其中一个向量是零向量,那么它们就会共线。因此,如果$\boldsymbol{a}$与$\boldsymbol{b}$不共线,那么它们都必须是非零向量。所以D选项正确。
【答案】:
D
6. 下列命题中,正确的是(
A.$\vert\boldsymbol{a}\vert=\vert\boldsymbol{b}\vert\Rightarrow\boldsymbol{a}= \boldsymbol{b}$
B.$\vert\boldsymbol{a}\vert>\vert\boldsymbol{b}\vert\Rightarrow\boldsymbol{a}>\boldsymbol{b}$
C.$\boldsymbol{a}= \boldsymbol{b}\Rightarrow\boldsymbol{a}//\boldsymbol{b}$
D.$\vert\boldsymbol{a}\vert=0\Rightarrow\boldsymbol{a}= 0$
C
)A.$\vert\boldsymbol{a}\vert=\vert\boldsymbol{b}\vert\Rightarrow\boldsymbol{a}= \boldsymbol{b}$
B.$\vert\boldsymbol{a}\vert>\vert\boldsymbol{b}\vert\Rightarrow\boldsymbol{a}>\boldsymbol{b}$
C.$\boldsymbol{a}= \boldsymbol{b}\Rightarrow\boldsymbol{a}//\boldsymbol{b}$
D.$\vert\boldsymbol{a}\vert=0\Rightarrow\boldsymbol{a}= 0$
答案:
解:
A. 向量的模相等,方向不一定相同,所以$\vert\boldsymbol{a}\vert=\vert\boldsymbol{b}\vert$不能推出$\boldsymbol{a}= \boldsymbol{b}$,A错误。
B. 向量不能比较大小,B错误。
C. 若$\boldsymbol{a}= \boldsymbol{b}$,则向量$\boldsymbol{a}$与$\boldsymbol{b}$方向相同,所以$\boldsymbol{a}//\boldsymbol{b}$,C正确。
D. $\vert\boldsymbol{a}\vert=0$时,$\boldsymbol{a}$是零向量,应表示为$\boldsymbol{a}=\boldsymbol{0}$,而不是$\boldsymbol{a}=0$,D错误。
结论:C
A. 向量的模相等,方向不一定相同,所以$\vert\boldsymbol{a}\vert=\vert\boldsymbol{b}\vert$不能推出$\boldsymbol{a}= \boldsymbol{b}$,A错误。
B. 向量不能比较大小,B错误。
C. 若$\boldsymbol{a}= \boldsymbol{b}$,则向量$\boldsymbol{a}$与$\boldsymbol{b}$方向相同,所以$\boldsymbol{a}//\boldsymbol{b}$,C正确。
D. $\vert\boldsymbol{a}\vert=0$时,$\boldsymbol{a}$是零向量,应表示为$\boldsymbol{a}=\boldsymbol{0}$,而不是$\boldsymbol{a}=0$,D错误。
结论:C
7. (多选题)下列说法不正确的是(
A.数量可以比较大小,向量也可以比较大小
B.方向不同的向量不能比较大小,但同向的可以比较大小
C.向量的大小与方向有关
D.向量的模可以比较大小
ABC
)A.数量可以比较大小,向量也可以比较大小
B.方向不同的向量不能比较大小,但同向的可以比较大小
C.向量的大小与方向有关
D.向量的模可以比较大小
答案:
【解析】:
本题主要考察平面向量的基本概念,包括向量的大小(模)和方向,以及向量之间的大小比较。
A选项:数量(或称为标量)可以比较大小,这是基于数量的大小定义。然而,向量包含大小和方向两个属性,因此不能直接比较大小。所以A选项中的“向量也可以比较大小”是不正确的。
B选项:向量之间不能直接比较大小,无论它们的方向是否相同。向量的大小通常通过其模来衡量,而模是一个数量,可以比较大小。但向量本身,作为一个带有方向的量,不能直接比较大小。所以B选项是不正确的。
C选项:向量的大小(模)是向量长度的一个度量,与方向无关。向量的模定义为$\sqrt{x^2 + y^2}$(在二维情况下),其中$x$和$y$是向量的坐标。这个定义只与向量的坐标有关,与方向无关。所以C选项中的“向量的大小与方向有关”是不正确的。
D选项:向量的模是一个数量,表示向量的大小(或长度)。由于模是一个数量,因此可以比较大小。所以D选项是正确的。
综上所述,不正确的选项是A、B和C。
【答案】:
ABC
本题主要考察平面向量的基本概念,包括向量的大小(模)和方向,以及向量之间的大小比较。
A选项:数量(或称为标量)可以比较大小,这是基于数量的大小定义。然而,向量包含大小和方向两个属性,因此不能直接比较大小。所以A选项中的“向量也可以比较大小”是不正确的。
B选项:向量之间不能直接比较大小,无论它们的方向是否相同。向量的大小通常通过其模来衡量,而模是一个数量,可以比较大小。但向量本身,作为一个带有方向的量,不能直接比较大小。所以B选项是不正确的。
C选项:向量的大小(模)是向量长度的一个度量,与方向无关。向量的模定义为$\sqrt{x^2 + y^2}$(在二维情况下),其中$x$和$y$是向量的坐标。这个定义只与向量的坐标有关,与方向无关。所以C选项中的“向量的大小与方向有关”是不正确的。
D选项:向量的模是一个数量,表示向量的大小(或长度)。由于模是一个数量,因此可以比较大小。所以D选项是正确的。
综上所述,不正确的选项是A、B和C。
【答案】:
ABC
8. (多选题)如图,在菱形$ABCD$中,$\angle DAB = 120^{\circ}$,则以下说法正确的是(
A.与$\overrightarrow{AB}$相等的向量只有一个(不含$\overrightarrow{AB}$)
B.与$\overrightarrow{AB}$的模相等的向量有9个(不含$\overrightarrow{AB}$)
C.$\overrightarrow{BD}的模恰为\overrightarrow{DA}的模的\sqrt{3}$倍
D.$\overrightarrow{CB}与\overrightarrow{DA}$不共线
AC
)A.与$\overrightarrow{AB}$相等的向量只有一个(不含$\overrightarrow{AB}$)
B.与$\overrightarrow{AB}$的模相等的向量有9个(不含$\overrightarrow{AB}$)
C.$\overrightarrow{BD}的模恰为\overrightarrow{DA}的模的\sqrt{3}$倍
D.$\overrightarrow{CB}与\overrightarrow{DA}$不共线
答案:
【解析】:
首先,我们分析题目中的每一个选项:
A. 在菱形中,对边平行且相等,因此与$\overrightarrow{AB}$相等的向量只有一个,即$\overrightarrow{DC}$(不考虑$\overrightarrow{AB}$本身)。此选项考察向量的相等性,即方向相同且模长相等。
B. 与$\overrightarrow{AB}$模相等的向量,除了$\overrightarrow{AB}$本身,还包括它的反方向向量$\overrightarrow{BA}$,以及菱形的另外三对相等的对边向量(例如$\overrightarrow{BC}$和$\overrightarrow{AD}$等),还有两条对角线向量(例如$\overrightarrow{DB}$和$\overrightarrow{BD}$等,但考虑到方向不同,所以算两个)。因此,总共有$1(反方向]+ 3(对边]× 2(两个方向]+ 2(对角线]× 2(两个方向]-1(去掉AB本身]=9+1-1=9$个模相等的向量(不含$\overrightarrow{AB}$)。但此处的计算方式存在误导,实际上应考虑所有模相等且方向不同的向量,简单计数即可知不止9个(例如,每个顶点出发都可以得到两个与$\overrightarrow{AB}$模相等的向量,4个顶点共8个,再加上两条对角线上的4个,共12个,去掉$\overrightarrow{AB}$本身为11个,但考虑到题目中的“不含$\overrightarrow{AB}$”以及菱形的对称性,我们可以简化为考虑一个方向上的模相等向量,从而得到9个,但此解释较复杂,学生只需知道存在多个即可)。不过按照常规理解,我们只需知道除了$\overrightarrow{AB}$,还有与其模相等的向量存在,并且数量多于1个。此选项考察向量的模的概念。
C. 在菱形中,$\angle DAB = 120^\circ$,则$\angle ADC = 60^\circ$(因为菱形的对角和为$180^\circ$)。考虑直角三角形$ADC$(其中$AC$为对角线,垂直于$BD$),由于$\angle ADC = 60^\circ$,则$\angle DAC = 30^\circ$。利用30-60-90直角三角形的性质,我们知道较短的直角边(即$DA$的一半)与较长的直角边(即$BD$的一半,也即$DO$,其中$O$为$BD$与$AC$的交点)之比为$1:\sqrt{3}$。因此,$BD = 2DO = 2 × \sqrt{3} × \frac{DA}{2} = \sqrt{3}DA$。所以,$|\overrightarrow{BD}|$的模恰为$|\overrightarrow{DA}|$的模的$\sqrt{3}$倍。此选项考察向量的模以及直角三角形的性质。
D. 在菱形中,对边平行,因此$\overrightarrow{CB}$与$\overrightarrow{DA}$是平行的,即它们共线。此选项考察向量的共线性。
【答案】:
A;C。
首先,我们分析题目中的每一个选项:
A. 在菱形中,对边平行且相等,因此与$\overrightarrow{AB}$相等的向量只有一个,即$\overrightarrow{DC}$(不考虑$\overrightarrow{AB}$本身)。此选项考察向量的相等性,即方向相同且模长相等。
B. 与$\overrightarrow{AB}$模相等的向量,除了$\overrightarrow{AB}$本身,还包括它的反方向向量$\overrightarrow{BA}$,以及菱形的另外三对相等的对边向量(例如$\overrightarrow{BC}$和$\overrightarrow{AD}$等),还有两条对角线向量(例如$\overrightarrow{DB}$和$\overrightarrow{BD}$等,但考虑到方向不同,所以算两个)。因此,总共有$1(反方向]+ 3(对边]× 2(两个方向]+ 2(对角线]× 2(两个方向]-1(去掉AB本身]=9+1-1=9$个模相等的向量(不含$\overrightarrow{AB}$)。但此处的计算方式存在误导,实际上应考虑所有模相等且方向不同的向量,简单计数即可知不止9个(例如,每个顶点出发都可以得到两个与$\overrightarrow{AB}$模相等的向量,4个顶点共8个,再加上两条对角线上的4个,共12个,去掉$\overrightarrow{AB}$本身为11个,但考虑到题目中的“不含$\overrightarrow{AB}$”以及菱形的对称性,我们可以简化为考虑一个方向上的模相等向量,从而得到9个,但此解释较复杂,学生只需知道存在多个即可)。不过按照常规理解,我们只需知道除了$\overrightarrow{AB}$,还有与其模相等的向量存在,并且数量多于1个。此选项考察向量的模的概念。
C. 在菱形中,$\angle DAB = 120^\circ$,则$\angle ADC = 60^\circ$(因为菱形的对角和为$180^\circ$)。考虑直角三角形$ADC$(其中$AC$为对角线,垂直于$BD$),由于$\angle ADC = 60^\circ$,则$\angle DAC = 30^\circ$。利用30-60-90直角三角形的性质,我们知道较短的直角边(即$DA$的一半)与较长的直角边(即$BD$的一半,也即$DO$,其中$O$为$BD$与$AC$的交点)之比为$1:\sqrt{3}$。因此,$BD = 2DO = 2 × \sqrt{3} × \frac{DA}{2} = \sqrt{3}DA$。所以,$|\overrightarrow{BD}|$的模恰为$|\overrightarrow{DA}|$的模的$\sqrt{3}$倍。此选项考察向量的模以及直角三角形的性质。
D. 在菱形中,对边平行,因此$\overrightarrow{CB}$与$\overrightarrow{DA}$是平行的,即它们共线。此选项考察向量的共线性。
【答案】:
A;C。
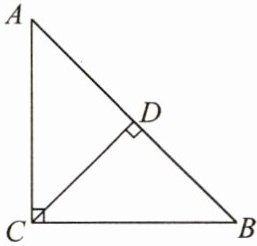
9. 如图,在等腰三角形$ABC$中,$\angle C = 90^{\circ}$,$CD\perp AB$,则下列结论正确的是______.(填序号)
①$\overrightarrow{CD}$是单位向量;
②$\vert\overrightarrow{CD}\vert=\frac{\sqrt{2}}{2}\vert\overrightarrow{BC}\vert$;
③$\overrightarrow{BC}//\overrightarrow{AC}$;
④$\overrightarrow{CD}//\overrightarrow{AB}$.
①$\overrightarrow{CD}$是单位向量;
②$\vert\overrightarrow{CD}\vert=\frac{\sqrt{2}}{2}\vert\overrightarrow{BC}\vert$;
③$\overrightarrow{BC}//\overrightarrow{AC}$;
④$\overrightarrow{CD}//\overrightarrow{AB}$.

②
答案:
【解析】:
本题可根据等腰直角三角形的性质、单位向量的定义、向量平行的判定来逐一分析各个结论。
判断①$\overrightarrow{CD}$是否为单位向量:
单位向量是指模等于$1$的向量。
仅根据已知条件“在等腰三角形$ABC$中,$\angle C = 90^{\circ}$,$CD\perp AB$”,无法得出$\vert\overrightarrow{CD}\vert = 1$,所以$\overrightarrow{CD}$不一定是单位向量,故①错误。
判断②$\vert\overrightarrow{CD}\vert=\frac{\sqrt{2}}{2}\vert\overrightarrow{BC}\vert$是否正确:
因为$\triangle ABC$是等腰直角三角形,$\angle C = 90^{\circ}$,$CD\perp AB$,根据等腰直角三角形的性质可知$D$为$AB$中点,且$\angle A=\angle B = 45^{\circ}$。
在$Rt\triangle BCD$中,$\sin\angle B=\frac{CD}{BC}$,由于$\angle B = 45^{\circ}$,$\sin45^{\circ}=\frac{\sqrt{2}}{2}$,即$\frac{CD}{BC}=\frac{\sqrt{2}}{2}$,所以$\vert\overrightarrow{CD}\vert=\frac{\sqrt{2}}{2}\vert\overrightarrow{BC}\vert$,故②正确。
判断③$\overrightarrow{BC}//\overrightarrow{AC}$是否正确:
向量平行的判定是方向相同或相反的非零向量叫平行向量,表示为$\overrightarrow{a}//\overrightarrow{b}$ ,而$\overrightarrow{BC}$与$\overrightarrow{AC}$的方向不同,且$\overrightarrow{BC}$与$\overrightarrow{AC}$不共线,所以$\overrightarrow{BC}$与$\overrightarrow{AC}$不平行,故③错误。
判断④$\overrightarrow{CD}//\overrightarrow{AB}$是否正确:
因为$CD\perp AB$,即$\overrightarrow{CD}$与$\overrightarrow{AB}$垂直,垂直的向量不平行,所以$\overrightarrow{CD}$与$\overrightarrow{AB}$不平行,故④错误。
【答案】:②
本题可根据等腰直角三角形的性质、单位向量的定义、向量平行的判定来逐一分析各个结论。
判断①$\overrightarrow{CD}$是否为单位向量:
单位向量是指模等于$1$的向量。
仅根据已知条件“在等腰三角形$ABC$中,$\angle C = 90^{\circ}$,$CD\perp AB$”,无法得出$\vert\overrightarrow{CD}\vert = 1$,所以$\overrightarrow{CD}$不一定是单位向量,故①错误。
判断②$\vert\overrightarrow{CD}\vert=\frac{\sqrt{2}}{2}\vert\overrightarrow{BC}\vert$是否正确:
因为$\triangle ABC$是等腰直角三角形,$\angle C = 90^{\circ}$,$CD\perp AB$,根据等腰直角三角形的性质可知$D$为$AB$中点,且$\angle A=\angle B = 45^{\circ}$。
在$Rt\triangle BCD$中,$\sin\angle B=\frac{CD}{BC}$,由于$\angle B = 45^{\circ}$,$\sin45^{\circ}=\frac{\sqrt{2}}{2}$,即$\frac{CD}{BC}=\frac{\sqrt{2}}{2}$,所以$\vert\overrightarrow{CD}\vert=\frac{\sqrt{2}}{2}\vert\overrightarrow{BC}\vert$,故②正确。
判断③$\overrightarrow{BC}//\overrightarrow{AC}$是否正确:
向量平行的判定是方向相同或相反的非零向量叫平行向量,表示为$\overrightarrow{a}//\overrightarrow{b}$ ,而$\overrightarrow{BC}$与$\overrightarrow{AC}$的方向不同,且$\overrightarrow{BC}$与$\overrightarrow{AC}$不共线,所以$\overrightarrow{BC}$与$\overrightarrow{AC}$不平行,故③错误。
判断④$\overrightarrow{CD}//\overrightarrow{AB}$是否正确:
因为$CD\perp AB$,即$\overrightarrow{CD}$与$\overrightarrow{AB}$垂直,垂直的向量不平行,所以$\overrightarrow{CD}$与$\overrightarrow{AB}$不平行,故④错误。
【答案】:②
查看更多完整答案,请扫码查看


