第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
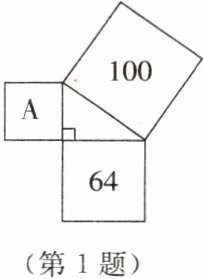
1. 如图,若 64,100 分别为所在正方形的面积,则正方形 A 的面积为
36
。
答案:
36
【解析】:本题主要考查勾股定理的应用。
根据勾股定理,在直角三角形中,两个直角边的平方和等于斜边的平方。
设正方形A的边长为a,已知另外两个正方形的面积分别为64和100,则它们的边长分别为$\sqrt{64}=8$和$\sqrt{100}=10。$
由于这三个正方形构成了一个直角三角形,其中边长为8和a的正方形是直角边,边长为10的正方形是斜边,所以可以根据勾股定理列出等式:
$a^2 + 8^2 = 10^2$
$a^2 = 100 - 64 = 36$
所以,正方形A的面积为$a^2 = 36 - 64 = 36。$
【答案】:36。
【解析】:本题主要考查勾股定理的应用。
根据勾股定理,在直角三角形中,两个直角边的平方和等于斜边的平方。
设正方形A的边长为a,已知另外两个正方形的面积分别为64和100,则它们的边长分别为$\sqrt{64}=8$和$\sqrt{100}=10。$
由于这三个正方形构成了一个直角三角形,其中边长为8和a的正方形是直角边,边长为10的正方形是斜边,所以可以根据勾股定理列出等式:
$a^2 + 8^2 = 10^2$
$a^2 = 100 - 64 = 36$
所以,正方形A的面积为$a^2 = 36 - 64 = 36。$
【答案】:36。
2. 长方形的一条对角线的长为 10 cm,一边长为 6 cm,它的面积是
48
cm²。
答案:
48
解:设长方形的另一条边长为 x cm。
因为长方形的对角线与两条邻边构成直角三角形,根据勾股定理可得:
$ 6^2 + x^2 = 10^2 $
$ 36 + x^2 = 100 $
$ x^2 = 100 - 36 = 64 $
x = 8 ( x = -8 舍去)
长方形面积 = 长×宽$ = 6×8 = 48 cm^2 $
答案:48
解:设长方形的另一条边长为 x cm。
因为长方形的对角线与两条邻边构成直角三角形,根据勾股定理可得:
$ 6^2 + x^2 = 10^2 $
$ 36 + x^2 = 100 $
$ x^2 = 100 - 36 = 64 $
x = 8 ( x = -8 舍去)
长方形面积 = 长×宽$ = 6×8 = 48 cm^2 $
答案:48
3. 在△ABC 中,∠C = 90°,a,b,c 分别为∠A,∠B,∠C 的对边。
(1)若 a = 5,b = 12,则 c² =
(2)若 c = 61,a = 60,则 b² =
(1)若 a = 5,b = 12,则 c² =
169
。(2)若 c = 61,a = 60,则 b² =
121
。
答案:
169
121
【解析】:
本题主要考察勾股定理的应用。在直角三角形中,直角边的平方和等于斜边的平方,即$a^2 + b^2 = c^2。$
(1) 已知直角边a和b的长度,需要求斜边c的平方。根据勾股定理,可以直接计算$c^2。$
(2) 已知斜边c和一条直角边a的长度,需要求另一条直角边b的平方。同样根据勾股定理,可以计算出$b^2。$
【答案】:
(1) 解:根据勾股定理,有$c^2 = a^2 + b^2。$
代入a = 5,b = 12,得$c^2 = 5^2 + 12^2 = 25 + 144 = 169。$
故答案为:$c^2 = 169。$
(2) 解:根据勾股定理,有$c^2 = a^2 + b^2。$
由此可得$b^2 = c^2 - a^2。$
代入c = 61,a = 60,得$b^2 = 61^2 - 60^2 = 3721 - 3600 = 121。$
故答案为:$b^2 = 121。$
121
【解析】:
本题主要考察勾股定理的应用。在直角三角形中,直角边的平方和等于斜边的平方,即$a^2 + b^2 = c^2。$
(1) 已知直角边a和b的长度,需要求斜边c的平方。根据勾股定理,可以直接计算$c^2。$
(2) 已知斜边c和一条直角边a的长度,需要求另一条直角边b的平方。同样根据勾股定理,可以计算出$b^2。$
【答案】:
(1) 解:根据勾股定理,有$c^2 = a^2 + b^2。$
代入a = 5,b = 12,得$c^2 = 5^2 + 12^2 = 25 + 144 = 169。$
故答案为:$c^2 = 169。$
(2) 解:根据勾股定理,有$c^2 = a^2 + b^2。$
由此可得$b^2 = c^2 - a^2。$
代入c = 61,a = 60,得$b^2 = 61^2 - 60^2 = 3721 - 3600 = 121。$
故答案为:$b^2 = 121。$
4. 我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦。若一个直角三角形中,勾为 9,股为 12,则弦为(
A.21
B.15
C.13
D.12
B
)A.21
B.15
C.13
D.12
答案:
B
解:根据勾股定理,弦长的平方等于勾长的平方加上股长的平方。
已知勾为9,股为12,设弦为c,则:
$c^2 = 9^2 + 12^2$
$c^2 = 81 + 144$
$c^2 = 225$
$c = \sqrt{225} = 15$
答案:B
解:根据勾股定理,弦长的平方等于勾长的平方加上股长的平方。
已知勾为9,股为12,设弦为c,则:
$c^2 = 9^2 + 12^2$
$c^2 = 81 + 144$
$c^2 = 225$
$c = \sqrt{225} = 15$
答案:B
5. 若直角三角形的两直角边长分别为 3 cm 和 4 cm,则斜边上的高为(
A.5 cm
B.4.8 cm
C.3 cm
D.2.4 cm
D
)A.5 cm
B.4.8 cm
C.3 cm
D.2.4 cm
答案:
D
解:
∵直角三角形两直角边长分别为3 cm和4 cm,
∴斜边长为$\sqrt{3^{2}+4^{2}}=5 cm。$
设斜边上的高为h cm,
由三角形面积公式得:$\frac{1}{2}×3×4=\frac{1}{2}×5× h,$
解得h=2.4。
答案:D
解:
∵直角三角形两直角边长分别为3 cm和4 cm,
∴斜边长为$\sqrt{3^{2}+4^{2}}=5 cm。$
设斜边上的高为h cm,
由三角形面积公式得:$\frac{1}{2}×3×4=\frac{1}{2}×5× h,$
解得h=2.4。
答案:D
6. 如图,在 Rt△ABC 中,∠ACB = 90°。若 AB = 13,则正方形 ADEC 与正方形 BCFG 的面积之和为(

A.25
B.144
C.169
D.以上都不对
C
)
A.25
B.144
C.169
D.以上都不对
答案:
C
【解析】:本题可根据勾股定理以及正方形面积公式来求解正方形ADEC与正方形BCFG的面积之和。
在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ},$根据勾股定理可知$AC^{2}+BC^{2}=AB^{2}。$
正方形ADEC的面积为$S_{ADEC}=AC^{2}($因为正方形面积等于边长的平方,这里边长为AC)。
正方形BCFG的面积为$S_{BCFG}=BC^{2}($同理,边长为BC)。
那么正方形ADEC与正方形BCFG的面积之和为$S_{ADEC}+S_{BCFG}=AC^{2}+BC^{2}。$
已知AB = 13,则$AB^{2}=13^{2}=169,$由勾股定理$AC^{2}+BC^{2}=AB^{2}=169,$即正方形ADEC与正方形BCFG的面积之和为169。
【答案】:C
【解析】:本题可根据勾股定理以及正方形面积公式来求解正方形ADEC与正方形BCFG的面积之和。
在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ},$根据勾股定理可知$AC^{2}+BC^{2}=AB^{2}。$
正方形ADEC的面积为$S_{ADEC}=AC^{2}($因为正方形面积等于边长的平方,这里边长为AC)。
正方形BCFG的面积为$S_{BCFG}=BC^{2}($同理,边长为BC)。
那么正方形ADEC与正方形BCFG的面积之和为$S_{ADEC}+S_{BCFG}=AC^{2}+BC^{2}。$
已知AB = 13,则$AB^{2}=13^{2}=169,$由勾股定理$AC^{2}+BC^{2}=AB^{2}=169,$即正方形ADEC与正方形BCFG的面积之和为169。
【答案】:C
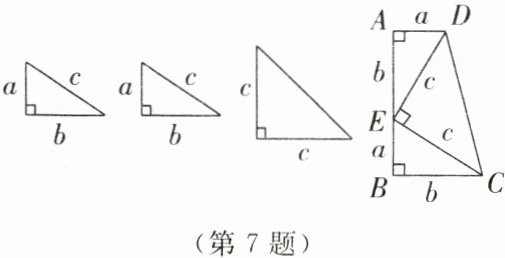
7. 在数学活动中,小明发现:两个直角边的长度分别为 a,b、斜边的长度为 c 的直角三角形和一个两条直角边的长度均为 c 的等腰直角三角形可以拼成一个直角梯形,如图所示。
(1)用两种不同的方法计算这个梯形的面积。a,b,c 之间有怎样的数量关系?请说明理由。
(2)若直角梯形的下底比上底长 1 cm,高为 7 cm,求△DEC 的面积。
(1)用两种不同的方法计算这个梯形的面积。a,b,c 之间有怎样的数量关系?请说明理由。
(2)若直角梯形的下底比上底长 1 cm,高为 7 cm,求△DEC 的面积。

答案:
解:
(1)利用梯形的面积公式计算
$\frac 12(a+b)(a+b)=\frac 12(a+b)^2$
用三个三角形面积的和计算
$\frac 12ab×2+\frac 12c×c=ab+\frac 12c^2$
∴$\frac 12(a+b)^2=ab+\frac 12c^2$
整理,得$a^2+b^2=c^2$
(2)由题可知,上底长为$a\mathrm {cm} ,$
则下底长$b=(a+1)\mathrm {cm}$
根据图形可知,a+a+1=7
解得a=3,b=4
∴$S_{△DEC}=\frac 12×(3^2+4^2)=\frac {25}2(\mathrm {cm}^2)$
(1)解:方法一:梯形面积公式
梯形上底为 a,下底为 b,高为 a+b,
面积$ S = \frac{1}{2}(a+b)(a+b) = \frac{1}{2}(a+b)^2 $
方法二:三个三角形面积之和
两个直角边为 a,b 的直角三角形面积和为$ 2 × \frac{1}{2}ab = ab,$
等腰直角三角形面积为$ \frac{1}{2}c^2,$
总面积$ S = ab + \frac{1}{2}c^2 $
由面积相等得:$\frac{1}{2}(a+b)^2 = ab + \frac{1}{2}c^2 $
化简得:$a^2 + b^2 = c^2 $
(2)解:由题意得:下底 b - 上底 a = 1,高 a + b = 7
解得 a = 3,b = 4
由
(1)知$ c^2 = a^2 + b^2 = 25,$则 c = 5
$\triangle DEC $面积为$ \frac{1}{2}c^2 = \frac{1}{2} × 25 = 12.5 \, cm^2 $
答案:$(1) a^2 + b^2 = c^2;$$(2) 12.5 \, cm^2$
(1)利用梯形的面积公式计算
$\frac 12(a+b)(a+b)=\frac 12(a+b)^2$
用三个三角形面积的和计算
$\frac 12ab×2+\frac 12c×c=ab+\frac 12c^2$
∴$\frac 12(a+b)^2=ab+\frac 12c^2$
整理,得$a^2+b^2=c^2$
(2)由题可知,上底长为$a\mathrm {cm} ,$
则下底长$b=(a+1)\mathrm {cm}$
根据图形可知,a+a+1=7
解得a=3,b=4
∴$S_{△DEC}=\frac 12×(3^2+4^2)=\frac {25}2(\mathrm {cm}^2)$
(1)解:方法一:梯形面积公式
梯形上底为 a,下底为 b,高为 a+b,
面积$ S = \frac{1}{2}(a+b)(a+b) = \frac{1}{2}(a+b)^2 $
方法二:三个三角形面积之和
两个直角边为 a,b 的直角三角形面积和为$ 2 × \frac{1}{2}ab = ab,$
等腰直角三角形面积为$ \frac{1}{2}c^2,$
总面积$ S = ab + \frac{1}{2}c^2 $
由面积相等得:$\frac{1}{2}(a+b)^2 = ab + \frac{1}{2}c^2 $
化简得:$a^2 + b^2 = c^2 $
(2)解:由题意得:下底 b - 上底 a = 1,高 a + b = 7
解得 a = 3,b = 4
由
(1)知$ c^2 = a^2 + b^2 = 25,$则 c = 5
$\triangle DEC $面积为$ \frac{1}{2}c^2 = \frac{1}{2} × 25 = 12.5 \, cm^2 $
答案:$(1) a^2 + b^2 = c^2;$$(2) 12.5 \, cm^2$
查看更多完整答案,请扫码查看


