第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1.下列说法:①等边三角形一定是等腰三角形,但等腰三角形不一定是等边三角形;②等腰三角形不可能是钝角三角形;③三角形按边分类可以分为等腰三角形和三边都不相等的三角形.其中正确的说法是
①③
(填序号).
答案:
【解析】:
本题主要考察三角形的分类及性质。
对于说法①:等边三角形的三边都相等,显然满足等腰三角形的定义(至少有两边相等),所以等边三角形一定是等腰三角形。但等腰三角形只要求至少有两边相等,并不要求三边都相等,所以等腰三角形不一定是等边三角形。因此,说法①是正确的。
对于说法②:等腰三角形只要求至少有两边相等,并不限制其角度大小。所以等腰三角形完全有可能是钝角三角形。因此,说法②是错误的。
对于说法③:三角形按边分类,确实可以分为等腰三角形(至少有两边相等)和三边都不相等的三角形。因此,说法③是正确的。
【答案】:
①③
本题主要考察三角形的分类及性质。
对于说法①:等边三角形的三边都相等,显然满足等腰三角形的定义(至少有两边相等),所以等边三角形一定是等腰三角形。但等腰三角形只要求至少有两边相等,并不要求三边都相等,所以等腰三角形不一定是等边三角形。因此,说法①是正确的。
对于说法②:等腰三角形只要求至少有两边相等,并不限制其角度大小。所以等腰三角形完全有可能是钝角三角形。因此,说法②是错误的。
对于说法③:三角形按边分类,确实可以分为等腰三角形(至少有两边相等)和三边都不相等的三角形。因此,说法③是正确的。
【答案】:
①③
2.如图所示,直线l经过A,B,C,D,E五点,点P是直线l外一点,连接PA,PB,PC,PD,PE,图中共有
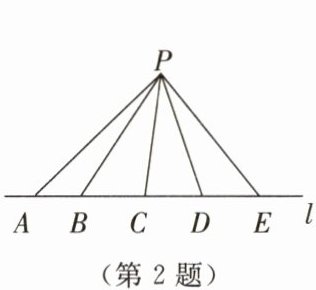
10
个三角形.
答案:
【解析】:本题可根据三角形的定义,通过数出由不同点组合形成的三角形个数来求解。
三角形是由同一平面内不在同一直线上的三条线段首尾顺次连接所组成的封闭图形。
在该图形中,以$PA$为一边的三角形有$\triangle PAB$、$\triangle PAC$、$\triangle PAD$、$\triangle PAE$;
以$PB$为一边且不重复的三角形有$\triangle PBC$、$\triangle PBD$、$\triangle PBE$;
以$PC$为一边且不重复的三角形有$\triangle PCD$、$\triangle PCE$;
以$PD$为一边且不重复的三角形有$\triangle PDE$。
将这些三角形的个数相加,即可得到图中三角形的总数。
【答案】:解:图中的三角形有$\triangle PAB$、$\triangle PAC$、$\triangle PAD$、$\triangle PAE$、$\triangle PBC$、$\triangle PBD$、$\triangle PBE$、$\triangle PCD$、$\triangle PCE$、$\triangle PDE$,共$10$个。
故答案为$10$。
三角形是由同一平面内不在同一直线上的三条线段首尾顺次连接所组成的封闭图形。
在该图形中,以$PA$为一边的三角形有$\triangle PAB$、$\triangle PAC$、$\triangle PAD$、$\triangle PAE$;
以$PB$为一边且不重复的三角形有$\triangle PBC$、$\triangle PBD$、$\triangle PBE$;
以$PC$为一边且不重复的三角形有$\triangle PCD$、$\triangle PCE$;
以$PD$为一边且不重复的三角形有$\triangle PDE$。
将这些三角形的个数相加,即可得到图中三角形的总数。
【答案】:解:图中的三角形有$\triangle PAB$、$\triangle PAC$、$\triangle PAD$、$\triangle PAE$、$\triangle PBC$、$\triangle PBD$、$\triangle PBE$、$\triangle PCD$、$\triangle PCE$、$\triangle PDE$,共$10$个。
故答案为$10$。
3.如图所示,以BD为边的三角形是
△ABD
;以∠DAC为一个内角的三角形是△ADC
;△AED的三个内角是∠AED, ∠ADE, ∠EAD
.
答案:
【解析】:
本题主要考查三角形的定义和内角的概念。
以BD为边的三角形,需要找到包含BD这条边的所有三角形。
以∠DAC为一个内角的三角形,需要找到包含∠DAC这个角的所有三角形。
△AED的三个内角,根据三角形内角和定理,一个三角形有三个内角,需要找出△AED的这三个内角。
以BD为边的三角形:
观察图形,BD边与点A和点C分别构成了三角形。
因此,以BD为边的三角形有△ABD和△BDC。
以∠DAC为一个内角的三角形:
观察图形,∠DAC是线段AD和线段DC的夹角。
包含∠DAC的三角形有△ADC和△ADE(因为E点在DC上,所以∠DAC也是△ADE的一个内角,但通常我们更关注最大的包含三角形,即△ADC)。但在此题中,更直接且完整的答案是△ADC,因为△ADE并不是以∠DAC为一个独立内角的唯一三角形(除非特别指出E点的位置对∠DAC有特殊影响,但题目并未如此说明)。
△AED的三个内角:
根据三角形内角和定理,△AED的三个内角分别是∠AED、∠ADE和∠EAD。
【答案】:
以BD为边的三角形是△ABD,
以∠DAC为一个内角的三角形是△ADC;
△AED的三个内角是∠AED, ∠ADE, ∠EAD。
本题主要考查三角形的定义和内角的概念。
以BD为边的三角形,需要找到包含BD这条边的所有三角形。
以∠DAC为一个内角的三角形,需要找到包含∠DAC这个角的所有三角形。
△AED的三个内角,根据三角形内角和定理,一个三角形有三个内角,需要找出△AED的这三个内角。
以BD为边的三角形:
观察图形,BD边与点A和点C分别构成了三角形。
因此,以BD为边的三角形有△ABD和△BDC。
以∠DAC为一个内角的三角形:
观察图形,∠DAC是线段AD和线段DC的夹角。
包含∠DAC的三角形有△ADC和△ADE(因为E点在DC上,所以∠DAC也是△ADE的一个内角,但通常我们更关注最大的包含三角形,即△ADC)。但在此题中,更直接且完整的答案是△ADC,因为△ADE并不是以∠DAC为一个独立内角的唯一三角形(除非特别指出E点的位置对∠DAC有特殊影响,但题目并未如此说明)。
△AED的三个内角:
根据三角形内角和定理,△AED的三个内角分别是∠AED、∠ADE和∠EAD。
【答案】:
以BD为边的三角形是△ABD,
以∠DAC为一个内角的三角形是△ADC;
△AED的三个内角是∠AED, ∠ADE, ∠EAD。
4.如图所示,在△ABC中,点D,E在线段BC上,AB= AC,AD= BD= AE= EC= DE.找出图中的等腰三角形和等边三角形.
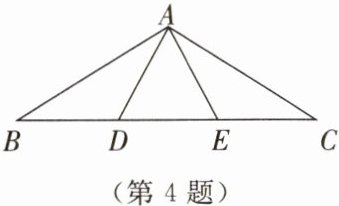

答案:
解:等腰三角形有:△ABC,△ABD,△AEC,△ADE
等边三角形有:△ADE。
等边三角形有:△ADE。
5.如图所示,在△ABC中,∠BAC= 90°,AD⊥BC于点D,图中一共有多少个三角形?分别找出图中的锐角三角形、直角三角形和钝角三角形.
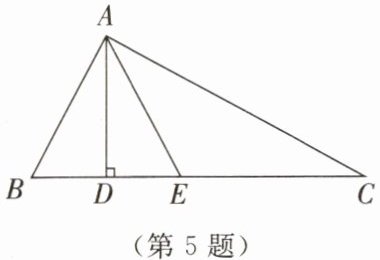

答案:
1. 首先数三角形个数:
图中的三角形有$\triangle ABC$,$\triangle ABD$,$\triangle ADE$,$\triangle AEC$,$\triangle ABE$,$\triangle ADC$,共$6$个。
2. 然后判断三角形类型:
锐角三角形:$\triangle ABE$
直角三角形:$\triangle ABC$,$\triangle ABD$,$\triangle ADE$,$\triangle ADC$。
钝角三角形:$\triangle AEC$。
综上,图中一共有$6$个三角形;锐角三角形是$\triangle ABE$;直角三角形是$\triangle ABC$,$\triangle ABD$,$\triangle ADE$,$\triangle ADC$;钝角三角形个数为$\triangle AEC$。
图中的三角形有$\triangle ABC$,$\triangle ABD$,$\triangle ADE$,$\triangle AEC$,$\triangle ABE$,$\triangle ADC$,共$6$个。
2. 然后判断三角形类型:
锐角三角形:$\triangle ABE$
直角三角形:$\triangle ABC$,$\triangle ABD$,$\triangle ADE$,$\triangle ADC$。
钝角三角形:$\triangle AEC$。
综上,图中一共有$6$个三角形;锐角三角形是$\triangle ABE$;直角三角形是$\triangle ABC$,$\triangle ABD$,$\triangle ADE$,$\triangle ADC$;钝角三角形个数为$\triangle AEC$。
6.如图所示,过A,B,C,D,E五个点中的任意三点画三角形.
(1)以AB为边画三角形,能画几个?写出各三角形的名称;
(2)分别指出(1)中画出的三角形,哪些是等腰三角形,哪些是钝角三角形.
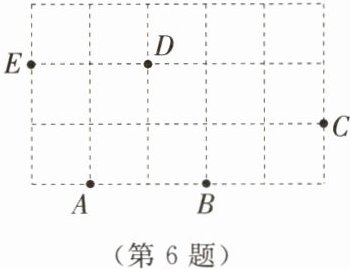
(1)以AB为边画三角形,能画几个?写出各三角形的名称;
(2)分别指出(1)中画出的三角形,哪些是等腰三角形,哪些是钝角三角形.

答案:
解:
(1)根据三角形的定义,以$AB$为边画三角形,从$C$、$D$、$E$中选一个点与$A$、$B$构成三角形。
能画$3$个三角形,分别是$\triangle ABC$、$\triangle ABD$、$\triangle ABE$。
(2)等腰三角形是$\triangle ABD$,钝角三角形是$\triangle ABC$,$\triangle ABE$。
(1)根据三角形的定义,以$AB$为边画三角形,从$C$、$D$、$E$中选一个点与$A$、$B$构成三角形。
能画$3$个三角形,分别是$\triangle ABC$、$\triangle ABD$、$\triangle ABE$。
(2)等腰三角形是$\triangle ABD$,钝角三角形是$\triangle ABC$,$\triangle ABE$。
查看更多完整答案,请扫码查看


