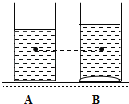
【题目】如图所示,水平桌面上有两个轻质圆柱形容器A、B,横截面积均为5.0×10﹣3米2,A的底面为平面,B的底面向上凸起.在两容器中均加入重为10牛的水,A对桌面的压强为 帕,A对桌面的压强 B对桌面的压强(选填“大于”、“小于”或“等于”).若A、B容器中同一水平高度处水的压强分别为pA、pB,则pA pB (选填“大于”、“小于”或“等于”).若在B中某一深度水的压强为1960帕,则该点的深度为 米.
参考答案:
【答案】2×103;小于;小于;0.2.
【解析】
试题分析:(1)根据水的重力为10N和横截面积均为5.0×10﹣3m2的容器,利用p=![]() 即可求出A对桌面的压强.
即可求出A对桌面的压强.
(2)A、B容器的自重忽略不计,它们对于水平桌面的压力等于各自所装的水重,因此只需判断出A、B两个容器底的底面积大小关系,结合压强公式p=![]() 即可判断出A、B容器对于桌面压强的大小关系.
即可判断出A、B容器对于桌面压强的大小关系.
(3)首先判断出两个容器液面的高度关系,由于所比较的是A、B容器的水中同一高度处的压强关系,所以要先判断出这两处距离各自液面的距离(即该点到液面的竖直高度),再由p=ρgh即可比较出两点所受压强的大小.
(4)由p=ρgh的变形式即可求出水的深度.
解:(1)A装有水10N,则对水平桌面的压力为:F=G=10N;
那么B容器对桌面的压强:p=![]() =
=![]() =2×103Pa.
=2×103Pa.
(2)A、B的质量忽略不计,而所装水量相同,因此它们对于桌面的压力都等于水的重力,即FA=FB=G=10N;
因为A的底面为平面,B的底面向上凸起,与桌面的接触面积关系为:SA>SB;
由p=![]() 得:A对桌面的压强小于B对桌面的压强.
得:A对桌面的压强小于B对桌面的压强.
(3)两容器的横截面积相同,所装水量相同,由于A的容器底向上凸出,所以A容器内的液面高度要小于B容器内的液面高度,即:hA<hB;
取两容器同一高度h处的两点,则这两点分别距A、B的液面高度为:HA=hA﹣h,HB=hB﹣h;
显然,HA<HB.
若A、B容器的水中同一高度处压强分别为pA、pB,则pA=ρgHA,pB=ρgHB
因为HA<HB,所以pA<pB.
(4)由p=ρgh得:在B中该点的深度h′=![]() =
=![]() =0.2m.
=0.2m.
故答案为:2×103;小于;小于;0.2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的电路中,电源电压为9伏且保持不变,电阻R1的阻值为10欧.闭合电键S后,电流表的示数变化了0.6安.求:
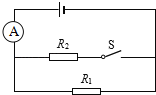
①通过R1的电流.
②R2的阻值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小方和小王设计的“测量食用油密度”的实验方案,请完善他们的方案,并回答后面的问题:
(1)小方的方案:用调节平衡的天平测出空烧杯的质量m1,向烧杯内倒入适量食用油,再测出烧杯和食用油的总质量m2,然后把烧杯内的食用油全部倒入量筒内,读出量筒内食用油的体积为V1;其测得的食用油密度的表达式是:
 油=______________.
油=______________.(2)小王的方案:在烧杯内倒入适量的食用油,用调节平衡的天平测出烧杯和食用油的总质量m3,然后将烧杯内的适量食用油倒入量筒内,再测出烧杯和剩余食用油的总质量m4,读出量筒内食用油的体积V2.其测得的食用油密度的表达式是:
 油=________.
油=________.(3)按_________(填“小方”、“小王”)的实验方案进行测量,实验误差可能小一些;如果选择另一种方案,测得的密度值________(填“偏大”、“偏小”).
(4)下图是按小王的实验方案进行某次实验的情况,请将实验的数据及测量结果填入表中.


-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家有一枚质量为2.1g的银币,他想用量筒测算出该银币是不是纯银的(ρ银=10.5g/cm3),所用的量筒规格如图所示,此量筒的分度值是________ml,请你根据实验的实际情况及相关数据分析:他能否鉴别出该银币?___________(选填“能”、“ 不能”),原因是____________________________。

-
科目: 来源: 题型:
查看答案和解析>>【题目】电阻R1=15Ω,R2=10Ω,R3=5Ω,下列连接电阻最小的是( )
A.只能用R3
B.R1与R3并联
C.R2与R3并联
D.R1、R2与R3并联 -
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学坐在过山车里,过山车高速运动时,小明看到地面上的人和建筑物都在旋转.他选取的参照物是( )
A.地面上的人 B.建筑物 C.过山车轨道 D.过山车
-
科目: 来源: 题型:
查看答案和解析>>【题目】导体的电阻是导体本身的一种性质.导体电阻的大小决定于导体的、和 , 还跟有关.
相关试题

