【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 在
在![]() 上,以
上,以![]() 为半径的⊙
为半径的⊙![]() 交
交![]() 于点
于点![]() ,
, ![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)判断直线![]() 与⊙
与⊙![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若![]() ,
, ![]() ,
, ![]() ,求线段
,求线段![]() 的长.
的长.

参考答案:
【答案】(1)直线DE与⊙O相切,理由见解析;
(2)DE的长为![]() .
.
【解析】(1)直线DE与⊙O相切,理由如下:连接OD,由OD=OA,利用等边对等角得到一对角相等,等量代换得到∠ODE为直角,即可得证;
(2)连接OE,设DE=x,则EB=ED=x,CE=8-x,在Rt△OCE中,利用勾股定理列出关于x的方程,求出方程得到x的值,即可确定出DE的长.
解:(1)直线DE与⊙O相切,理由如下:
连接OD,

∵OD=OA,∴∠A=∠ODA,
∵EF是BD的垂直平分线,
∴EB=ED, ∴∠B=∠EDB,
∵∠C=90°,∴∠A+∠B=90°,
∴∠ODA+∠EDB=90°,
∴∠ODE=180°﹣90°=90°,
∴直线DE与⊙O相切;
(2)连接OE,
设DE=x,则EB=ED=x,CE=8﹣x,
∵∠C=∠ODE=90°,∴OC2+CE2=OE2=OD2+DE2,
∴42+(8﹣x)2=22+x2,
解得: ![]() , 则DE=
, 则DE=![]() .
.
“点睛”本题考查了直线与圆的位置关系,以及线段垂直平分线定理,熟练掌握直线与圆相切的性质是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=x2先向右平移2个单位长度,再向上平移3个单位长度,平移后的抛物线的解析式是______________。
-
科目: 来源: 题型:
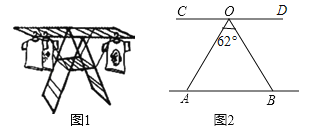
查看答案和解析>>【题目】小梅家的阳台上放置了一个晒衣架如图1,图2是晒衣架的侧面示意图,A,B两点立于地面,将晒衣架稳固张开,测得张角∠AOB=62°,立杆OA=OB=140cm,小梅的连衣裙穿在衣架后的总长度为122cm,问将这件连衣裙垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由(参考数据:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2﹣2x﹣k=0有两个相等的实数根,则k的值为( )
A.﹣1B.﹣2C.1D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】合并同类项:
(1)x3﹣2x2﹣x3+5x2+4;
(2)4xy﹣3x2﹣3xy﹣2y+2x2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+x+2=0的根的情况是( )
A.两个相等的实数根B.两个不相等的实数根
C.无实数根D.无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】六个正整数的中位数是4.5,众数是7,极差是6,这六个正整数的和为________.
相关试题

