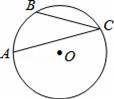
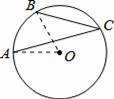
如图，点A、B、C在半径为9的⊙O上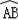，的长为2π，则∠ACB的大小是　　．


20°【考点】弧长的计算；圆周角定理．

【分析】连结OA、OB．先由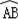的长为2π，利用弧长计算公式求出∠AOB=40°，再根据在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半得到∠ACB=∠AOB=20°．

【解答】解：连结OA、OB．设∠AOB=n°．

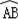
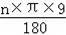
∵的长为2π，

∴=2π，

∴n=40，

∴∠AOB=40°，

∴∠ACB=∠AOB=20°．

故答案为20°．

【点评】本题考查了弧长公式：l=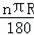（弧长为l，圆心角度数为n，圆的半径为R），同时考查了圆周角定理．


关闭