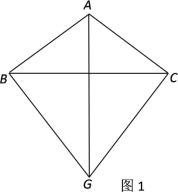
【题目】如图1,在△ABC中,AB=AC,G为三角形外一点,且△GBC为等边三角形.
(1)求证:直线AG垂直平分BC;
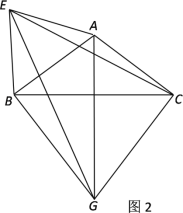
(2)以AB为一边作等边△ABE(如图2),连接EG、EC,试判断△EGC是否构成直角三角形?请说明理由.
参考答案:
【答案】(1)证明见解析(2)△EGC构成直角三角形
【解析】
(1)由GB=GC,得出点G在BC的垂直平分线上,同理得出点A在BC的垂直平分线上,即可得出结论;
(2)由等边三角形的性质得出GB=BC=GC, EB=BA,∠EBA=∠GBC=∠BGC=∠BCG =60°,证出∠EBC=∠ABG,由SAS证明△EBC≌△ABG,得出∠ECB=∠AGB,再由等腰三角形的性质即可得出结论.
(1)∵△GBC为等边三角形,∴GB=GC,
∴点G在BC的垂直平分线上,
又∵AB=AC,∴点A在BC的垂直平分线上,
∴直线AG垂直平分BC;
(2)△EGC构成直角三角形,
∵△GBC和△ABE为等边三角形,
∴GB=BC=GC,EB=BA,∠EBA=∠GBC=∠BGC=∠BCG =60°,
∴∠EBC=∠ABG,∴△EBC≌△ABG ,
∴∠ECB=∠AGB,∵GB=GC且AG⊥BC,∴∠AGB=![]() ∠BGC=30°,
∠BGC=30°,
∴∠ECB=30°,
∴∠ECG=90°,即△EGC构成直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB∥DF,∠D+∠B=180°,

(1)求证:DE∥BC;
(2)如果∠AMD=75°,求∠AGC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1(注:与图2完全相同),二次函数y=
 x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.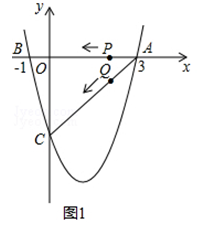
(1)求该二次函数的解析式;
(2)设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);
(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).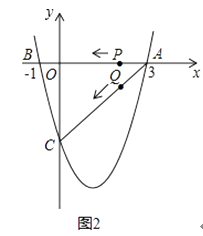
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,若AB=17,BD=12,
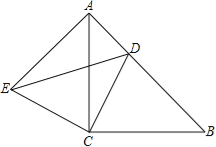
(1)求证:△BCD≌△ACE;
(2)求DE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏,下列命题中错误的是( )

A.红红不是胜就是输,所以红红胜的概率为
B.红红胜或娜娜胜的概率相等
C.两人出相同手势的概率为
D.娜娜胜的概率和两人出相同手势的概率一样 -
科目: 来源: 题型:
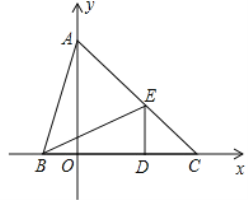
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(0,b),点B(a,0),点D(2,0),其中a、b满足
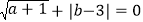 , DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.
, DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.(1)求A、B、E三点的坐标;
(2) 若以AB为一边在第二象限内构造等腰直角三角形△ABF,请直接写出点F的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.
(1)求∠BOD的度数;
(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.

相关试题

