【题目】如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为m. 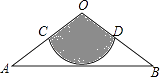
参考答案:
【答案】20 ![]()
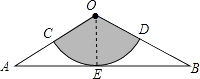
【解析】解:过O作OE⊥AB于E,∵OA=OB=60cm,∠AOB=120°, ∴∠A=∠B=30°,
∴OE= ![]() OA=30cm,
OA=30cm,
∴弧CD的长= ![]() =20π,
=20π,
设圆锥的底面圆的半径为r,则2πr=20π,解得r=10,
∴圆锥的高= ![]() =20
=20 ![]() .
.
故答案为:20 ![]() .
.
根据等腰三角形的性质得到OE的长,再利用弧长公式计算出弧CD的长,设圆锥的底面圆的半径为r,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长得到r,然后利用勾股定理计算出圆锥的高.
-
科目: 来源: 题型:
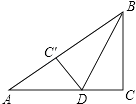
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是( )
A.3cm2
B.4cm2
C.5cm2
D.6cm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是( )
A.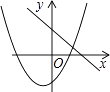
B.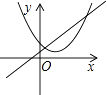
C.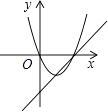
D.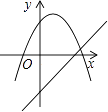
-
科目: 来源: 题型:
查看答案和解析>>【题目】P是等边△ABC内部一点,∠APB、∠BPC、∠CPA的大小之比是5:6:7,将△ABP逆时针旋转,使得AB与AC重合,则以PA、PB、PC的长为边的三角形的三个角∠PCQ:∠QPC:∠PQC= .
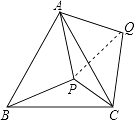
-
科目: 来源: 题型:
查看答案和解析>>【题目】某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行?为什么?

-
科目: 来源: 题型:
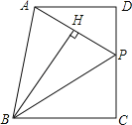
查看答案和解析>>【题目】如图,已知四边形ABCD中,AD∥BC,∠C=90°,P是CD上一点,BH⊥AP于H,BH=BC=CD
(1)求证:∠ABP=45°;
(2)若BC=20,PC=12,求AP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数
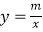 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.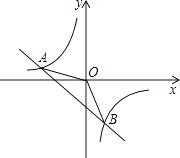
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB的面积.
相关试题

