【题目】若等腰三角形的周长为26,一边为11,则腰长为( ).
A. 11B. 7.5C. 11或7.5D. 以上都不对
参考答案:
【答案】C
【解析】
已知的边长11可能是腰也可能是底,所以分两种情况讨论,一种是11为腰,则另一腰长也为11,再根据周长为26即可得出三边长度,再用三角形三边关系验证能否组成三角形即可;另一种是11为底,则可求出两腰长得和,就可以求出腰长,得出三边长度,再用三角形三边关系验证能否组成三角形即可.
解:由题可知等腰三角形一边长为11,分以下两种情况:
①若11为腰,则另一腰长也为11,第三边长为![]() ;
;
所以等腰三角形三边长为11,11,4,可以构成三角形;
②若11为底,则两腰长为![]() ;
;
所以等腰三角形三边长为7.5,7.5,11,可以构成三角形;
综上所述,此等腰三角形的腰长为11或7.5;
故答案选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于
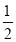 BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( ) 
A. 90°B. 95°C. 100°D. 105°
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:对任意一个两位数
 ,如果
,如果 满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“迥异数”,将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为
满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“迥异数”,将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为 .例如:
.例如: ,对调个位数字与十位数字得到新两位数21,新两位数与原两位数的和为21+12=33,和与11的商为33÷11=3,所以
,对调个位数字与十位数字得到新两位数21,新两位数与原两位数的和为21+12=33,和与11的商为33÷11=3,所以 .根据以上定义,回答下列问题:
.根据以上定义,回答下列问题:(1)填空:①下列两位数:40,42,44中,“迥异数”为_______;②计算:
 =_______;
=_______;(2)如果一个“迥异数”
 的十位数字是
的十位数字是 ,个位数字是
,个位数字是 ,且
,且 ,请求出“迥异数”
,请求出“迥异数” .
. -
科目: 来源: 题型:
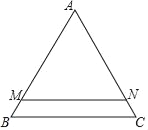
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠A=60°,BC=6,直线MN∥BC,且分别交边AB,AC于点M,N,已知直线MN将△ABC分为△AMN和梯形MBCN面积之比为5:1的两部分,如果将线段AM绕着点A旋转,使点M落在边BC上的点D处,那么BD=_____.
-
科目: 来源: 题型:
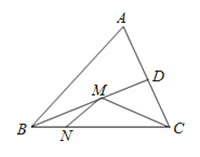
查看答案和解析>>【题目】在锐角△ABC中,∠ABC=60°,BC=2cm,BD平分∠ABC交AC于点D,点M,N分别是BD和BC边上的动点,则MN+MC的最小值是( ).
A.
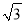 B.
B. 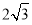 C.
C. 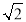 D.
D. 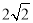
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB,AC的垂直平分线交BC于点E,G,若∠B+∠C=70°,则∠EAG=___.

-
科目: 来源: 题型:
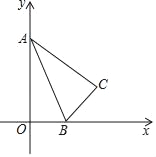
查看答案和解析>>【题目】如图,Rt△ABC中,BC=4,AC=8,Rt△ABC的斜边在x轴的正半轴上,点A与原点重合,随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束.在这个运动过程中.
(1)AB中点P经过的路径长_____.
(2)点C运动的路径长是_____.
相关试题

