Question

【题目】已知，在中， ．过A点的直线从与边重合的位置开始绕点按顺时针方向旋转角，直线交BC边于点（点不与点、点重合），的边始终在直线上（点在点的上方），且，连接。

（1）当时，

①如图a，当时，求的度数；

②如图b，当时， 的度数是否发生变化？说明理由.

（2）如图c，当时，请直接写出与之间的数量关系，不必证明.

Answer 1

【答案】（1）①∠ANC=45°；②当θ≠45°时，①中的结论不发生变化． 理由见解析

（2）∠ANC=90°﹣∠BAC．理由见解析

【解析】试题分析：（1）①证明四边形ABNC是正方形，根据正方形的对角线平分一组对角线即可求解；②根据等腰直角三角形的性质可得∠BNP=∠ACB，然后证明△BNP和△ACP相似，根据相似三角形对应边成比例可得，再根据两边对应成比例夹角相等可得△ABP和△CNP相似，然后根据相似三角形对应角相等可得∠ANC=∠ABC，从而得解；

（2）根据等腰三角形的两底角相等求出∠BNP=∠ACB，然后证明△BNP和△ACP相似，根据相似三角形对应边成比例可得，再根据两边对应成比例夹角相等可得△ABP和△CNP相似，然后根据相似三角形对应角相等可得∠ANC=∠ABC，然后根据三角形的内角和定理列式整理即可得解．

试题解析：（1）①∵∠BAC=90°，θ=45°，

∴AP⊥BC，BP=CP（等腰三角形三线合一），

∴AP=BP（直角三角形斜边上的中线等于斜边的一半），

又∵∠MBN=90°，BM=BN，

∴AP=PN（等腰三角形三线合一），

∴AP=PN=BP=PC，且AN⊥BC，

∴四边形ABNC是正方形，

∴∠ANC=45°；

②连接CN，

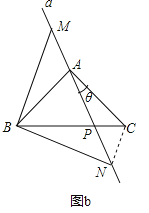
当θ≠45°时，①中的结论不发生变化．理由如下：

∵∠BAC=∠MBN=90°，AB=AC，BM=BN，

∴∠ABC=∠ACB=∠BNP=45°，

又∵∠BPN=∠APC，

∴△BNP∽△ACP，

∴，

又∵∠APB=∠CPN，

∴△ABP∽△CNP，

∴∠ANC=∠ABC=45°；

（2）∠ANC=90°﹣∠BAC．理由如下：

∵∠BAC=∠MBN≠90°，AB=AC，BM=BN，

∴∠ABC=∠ACB=∠BNP=（180°﹣∠BAC），

又∵∠BPN=∠APC，

∴△BNP∽△ACP，

∴，

又∵∠APB=∠CPN，

∴△ABP∽△CNP，

∴∠ANC=∠ABC，

在△ABC中，

∠ABC=（180°﹣∠BAC）=90°﹣∠BAC．