【题目】在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 三边的长分别为
三边的长分别为![]() ,
, ![]() ,
, ![]() ,求这个三角形的面积.
,求这个三角形的面积.
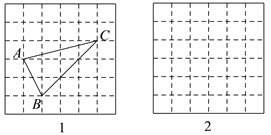
小明同学在解答这道题时,先建立了一个正方形网格(每个小正方形的边长为1),再在网格中
画出格点△ABC中,(即△ABC三个顶点都在小正方形的顶点处),如图1所示,这样不需要△ABC高,借用网格就能计算出它的面积.
(1)△ABC的面积为 ;
(2)如果△MNP三边的长分别为![]() ,
, ![]() ,
, ![]() ,请利用图2的正方形网格(每个小正方形的边长为1)画出相应的格点△MNP,并直接写出△MNP的面积为 .
,请利用图2的正方形网格(每个小正方形的边长为1)画出相应的格点△MNP,并直接写出△MNP的面积为 .
参考答案:
【答案】(1)4.5;(2)作图见解析,7.
【解析】试题分析:(1)根据网格图结合割补法可得:S△ABC=S矩形MONC-S△CMA-S△AOB-S△BNC=12-2-1-4.5=4.5;(2)利用割补法可得:S△MNP=S矩形BMOA-S△BMP-S△MON-S△ANP= 15-1.5-2.5-4=7.
试题解析:
(1)
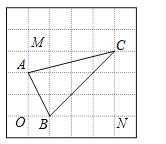
S△ABC=S矩形MONC-S△CMA-S△AOB-S△BNC=12-2-1-4.5=4.5;
(2)
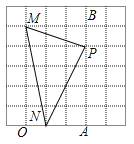
S△MNP=S矩形BMOA-S△BMP-S△MON-S△ANP= 15-1.5-2.5-4=7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲组的4名工人3月份完成的总工作量比此月人均定额的4倍多20件,乙组的5名工人3月份完成的总工作量比此月人均定额的6倍少20件.
(1)如果两组工人实际完成的此月人均工作量相等,那么此月人均定额是多少件?
(2)如果甲组工人实际完成的此月人均工作量比乙组的多2件,则此月人均定额是多少件?
(3)如果甲组工人实际完成的此月人均工作量比乙组的少2件,则此月人均定额是多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果+60m表示“向北走60m”,那么“向南走40m”可以表示为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式不成立的是( )
A.(-3)3=-33B.-24=(-2)4C.|-3|=|3|D.(-3)100=3100
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格;

(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于
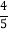 ,求m的值.
,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,点D为BC中点,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.求证:四边形ADCE为矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:-6ab+ba+8ab的结果是 ( )
A.2abB.3C.-3abD.3ab
相关试题

