【题目】如图,△ABC中,∠B=∠C=∠EDF=α,BD=CF,BE=CD,则下列结论正确的是( )
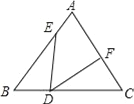
A. 2α+∠A=180° B. α+∠A=90° C. 2α+∠A=90° D. α+∠A=180°
参考答案:
【答案】A
【解析】根据三角形内角和定理即可判断.
解:A、正确.∵∠A+∠B+∠C=180°,∠B=∠C=α,∴2α+∠A=180°.
B、错误.不妨设,α+∠A=90°,∵2α+∠A=180°,∴α=90°,这个显然与已知矛盾,故结论不成立.
C、错误.∵2α+∠A=180°,∴2α+∠A=90°不成立.
D、错误.∵2α+∠A=180°,∴α+∠A=180°不成立.
故选A.
“点睛”本题考查三角形内角和定理,解题的关键是灵活运用三角形内角和定理,属于基础题,中考常考题型.
-
科目: 来源: 题型:
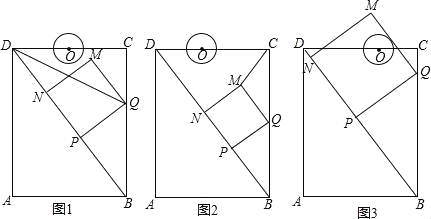
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3m/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单位:s)(0<t<).
(1)如图1,连接DQ平分∠BDC时,t的值为 ;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果代数式2y2﹣y的值是1,那么代数式8y2﹣4y+1的值等于_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示0.00000022是( )
A.0.22×10﹣6B.2.2×107C.2.2×10﹣6D.2.2×10﹣7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示, AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A=70°,∠B=55°,则△ABC是( )
A. 钝角三角形 B. 等腰三角形
C. 等边三角形 D. 等腰直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据21、12、18、16、20、21的众数和中位数分别是( )
A.21和19B.21和17C.20和19D.20和18
相关试题

