【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
参考答案:
【答案】(1)、y=-![]() +24x+3200;(2)、200元;(2)、150元,5000元.
+24x+3200;(2)、200元;(2)、150元,5000元.
【解析】
试题分析:(1)、根据总利润=单件利润×数量得出函数关系式;(2)、将y=4800代入函数解析式,求出x的值,然后根据题意进行验根;(3)、将二次函数进行配成顶点式,然后得出最值.
试题解析:(1)、根据题意,得y=(2400﹣2000﹣x)(8+4×![]() ), 即y=﹣
), 即y=﹣![]() x2+24x+3200;
x2+24x+3200;
(2)、由题意得﹣![]() x2+24x+3200=4800. 整理,得x2﹣300x+20000=0. 解这个方程,得x1=100,x2=200.
x2+24x+3200=4800. 整理,得x2﹣300x+20000=0. 解这个方程,得x1=100,x2=200.
要使百姓得到实惠,取x=200元. ∴每台冰箱应降价200元;
(3)、对于y=﹣![]() x2+24x+3200=﹣
x2+24x+3200=﹣![]() (x﹣150)2+5000, 当x=150时, y最大值=5000(元).
(x﹣150)2+5000, 当x=150时, y最大值=5000(元).
所以,每台冰箱的售价降价150元时,商场的利润最大,最大利润是5000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB,王华同学按下列步骤作图:(1)以点O为圆心,任意长为半径作弧,交OA于点C,交OB于点D,分别以点C、点D为圆心,大于
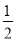 CD的长为半径作弧,两弧交于点E,作射线OE;(2)在射线OE上取一点F,分别以点O、点F为圆心,大于
CD的长为半径作弧,两弧交于点E,作射线OE;(2)在射线OE上取一点F,分别以点O、点F为圆心,大于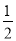 OF的长为半径作弧,两弧交于两点G、H,作直线GH,交OA于点M,交OB于点N;(3)连接FM、FN.那么四边形OMFN一定是( )
OF的长为半径作弧,两弧交于两点G、H,作直线GH,交OA于点M,交OB于点N;(3)连接FM、FN.那么四边形OMFN一定是( )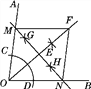
A. 梯形 B. 矩形 C. 菱形 D. 正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于a,b的多项式3(a2﹣2ab﹣b2)﹣(a2+mab+2b2)中不含有ab项,则m= .
-
科目: 来源: 题型:
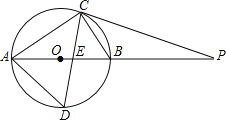
查看答案和解析>>【题目】如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)
(1)如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某品牌电风扇销售量的情况,对某商场5月份该品牌甲、乙、丙三种型号的电风扇销售量进行统计,绘制如下两个统计图(均不完整).请你结合图中的信息,解答下列问题:
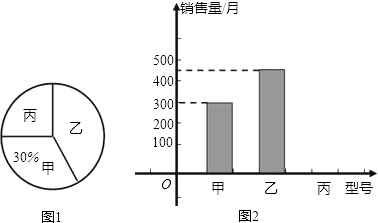
(1)该商场5月份售出这种品牌的电风扇共多少台?
(2)若该商场计划订购这三种型号的电风扇共2000台,根据5月份销售量的情况,求该商场应订购丙种型号电风扇多少台比较合理? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知2a+b=23,a+2b=25,则代数式a+b=________.
相关试题

