【题目】一元二次方程x2+x﹣2=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根
参考答案:
【答案】A
【解析】解:△=b2﹣4ac=12﹣4×1×(﹣2)=9,
∵9>0,
∴原方程有两个不相等的实数根.
所以答案是:A
【考点精析】本题主要考查了求根公式的相关知识点,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 分解因式:9a﹣a3=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数中,立方根一定是负数的是( )
A. —a B. —a2 C. —a2-1 D. —a2+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数的算术平方根与它的立方根的值相同,则这个数是( )
A. 1 B. 0或1 C. 0 D. 非负数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形。


(1)你认为图2中的阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图2中阴影部分的面积:
方法1: ;
方法2: ;
(3)观察图2你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2,(m-n)2,mn. ;
(4)根据(3)题中的等量关系,解决如下问题:
若a+b=7,ab=5,则(a-b)2== 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】将若干张长为20厘米、宽为10厘米的长方形白纸,按图9所示的方法粘合起来,粘合部分的宽为2厘米.
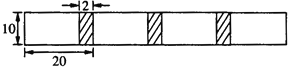
(1)求4张白纸粘合后的总长度;
(2)设x张白纸粘合后的总长度为y厘米,写出y与x之间的关系式,并求当x=20时,y的值.
-
科目: 来源: 题型:
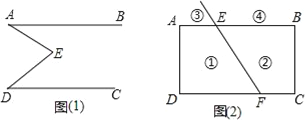
查看答案和解析>>【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)
相关试题

