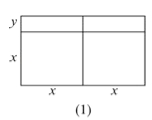
【题目】大家已经知道，完全平方公式和平方差公式可以用平面几何图形的面积来表示，实际上还有一些代数恒等式也可以用这种形式表示，例如：2x（x+y）=2x2+2xy就可以用图的面积表示．

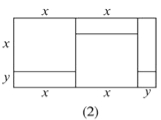
（1）请写出图（2）所表示的代数恒等式：　_______　；

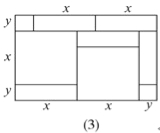
（2）请写出图（3）所表示的代数恒等式：　________　；

（3）试画出一个几何图形，使它的面积能表示（x+y）（x+3y）=x2+4xy+3y2．

参考答案：

【答案】（1）2x2+3xy+y2 （2）（x+2y）（2x+y）=2x2+5xy+2y2 （3）x2+4xy+3y2

【解析】

试题分析：（1）图（2）中，大长方形边长为（x+y），（2x+y），图形中包括了两个边长为x的正方形，三个边长为x、y的长方形，一个边长为y的正方形，根据面积关系得出代数恒等式；

（2）图（3）中，大长方形边长为（x+2y），（2x+y），图形中包括了两个边长为x的正方形，五个边长为x、y的长方形，二个边长为y的正方形，根据面积关系得出代数恒等式；

（3）根据题意，画出边长为（x+y），（x+3y）的长方形，再将图形划分，利用面积关系说明等式．

解：（1）由图（2）的面积关系可知，（x+y）（2x+y）=2x2+3xy+y2；

故答案为：2x2+3xy+y2；

（2）由图（3）的面积关系可知，（x+2y）（2x+y）=2x2+5xy+2y2；

故答案为：（x+2y）（2x+y）=2x2+5xy+2y2；

（3）以边长为（x+y），（x+3y）画长方形，如图所示，

由图可知，（x+y）（x+3y）=x2+4xy+3y2．

关闭