【题目】如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=8,AB=CD=17.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为______.
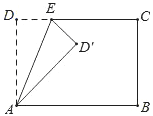
参考答案:
【答案】2或32.
【解析】分两种情况:点E在DC线段上,点E为DC延长线上的一点,进一步分析探讨得出答案即可.
解:如图1,
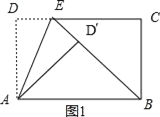
∵折叠,∴△AD′E≌△ADE,∴∠AD′E=∠D=90°,∵∠AD′B=90°,∴B、D′、E三点共线,
又∵ABD′∽△BEC,AD′=BC,∴ABD′≌△BEC,∴BE=AB=17,
∵BD′=![]() =15,
=15,
∴DE=D′E=17﹣15=2;
如图2,
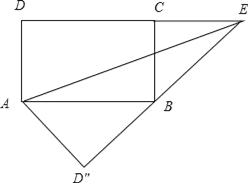
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,
∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
∠D″=∠BCE,AD″=BC,∠CBE=∠BAD″,
∴△ABD″≌△BEC,
∴BE=AB=17,
∴DE=D″E=17+15=32.
综上所知,DE=2或32.
故答案为:2或32.
“点睛”翻折的性质,三角形全等的判定与性质,勾股定理,掌握翻折的性质,分类探讨的思想方法是解决问题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x+5>4x﹣1的正整数解是
-
科目: 来源: 题型:
查看答案和解析>>【题目】铁路部门规定旅客免费携带行李箱的长、宽、高之和不超过160cm,某厂家生产符合该规定的行李箱,已知行李箱的高为30cm,长与宽的比为3:2,则该行李箱的长的最大值为多少厘米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P(m,m-3)在第三象限,则字母m的取值范围为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=
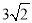 ,CD=
,CD=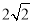 ,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为
,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为 ,则满足条件的点P有 个.
,则满足条件的点P有 个.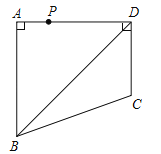
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个矩形ABCD及⊙M给出如下定义:在同一平面内,如果矩形ABCD的四个顶点到⊙M上一点的距离相等,那么称这个矩形ABCD是⊙M的“伴侣矩形”.如图,在平面直角坐标系xOy中,直线l:
 交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .
交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .
-
科目: 来源: 题型:
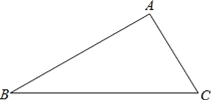
查看答案和解析>>【题目】在△ABC中,AB=8,BC=10,AC=6,动点P从点C出发,沿着CB运动,速度为每秒2个单位,到达点B时运动停止,设运动时间为t秒,请解答下列问题:
(1)求BC上的高;
(2)当t为何值时,△ACP为等腰三角形?
相关试题

