Question

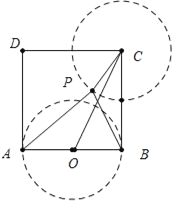
【题目】已知正方形ABCD的边长为1，点P为正方形内一动点，若点M在AB上，且满足△PBC∽△PAM，延长BP交AD于点N，连结CM．

（1）如图一，若点M在线段AB上，求证：AP⊥BN；AM=AN；

（2）①如图二，在点P运动过程中，满足△PBC∽△PAM的点M在AB的延长线上时，AP⊥BN和AM=AN是否成立？

②是否存在满足条件的点P，使得PC=？（不需说明理由）．

Answer 1

【答案】（1）证明见解析；（2）①仍然成立，AP⊥BN和AM=AN． ②这样的点P不存在．

【解析】试题分析：（1）根据相似三角形的性质得到∠PAM=∠PBC，根据正方形的性质证明，得到AP⊥BN，根据相似三角形的对应边的比线段求出AM与AN的数量关系；

（2）①同（1）的证明方法类似；

②根据圆周角定理得到点P在以AB为直径的圆上，根据勾股定理计算即可．

试题解析：（1）如图一中，∵四边形ABCD是正方形，∴AB=BC=CD=AD，∠DAB=∠ABC=∠BCD=∠D=90°，

∵△PBC∽△PAM，∴∠PAM=∠PBC， ，∴∠PBC+∠PBA=90°，∴∠PAM+∠PBA=90°，

∴∠APB=90°，∴AP⊥BN，∵∠ABP=∠ABN，∠APB=∠BAN=90°，

∴△BAP∽△BNA，∴，∴，∵AB=BC，∴AN=AM．

（2）①仍然成立，AP⊥BN和AM=AN．

理由如图二中，∵四边形ABCD是正方形，∴AB=BC=CD=AD，∠DAB=∠ABC=∠BCD=∠D=90°，

∵△PBC∽△PAM， ∴∠PAM=∠PBC， ，∴∠PBC+∠PBA=90°，

∴∠PAM+∠PBA=90°， ∴∠APB=90°，∴AP⊥BN，∵∠ABP=∠ABN，∠APB=∠BAN=90°，

∴△BAP∽△BNA，∴，∴，∵AB=BC，∴AN=AM．

②这样的点P不存在．理由：假设PC=，如图三中，以点C为圆心为半径画圆，以AB为直径画圆， CO= = ＞1+，∴两个圆无公共点，∴∠APB＜90°，这与AP⊥PB矛盾，

∴假设不可能成立，∴满足PC=的点P不存在．