【题目】通过电脑拨号上“因特网”的费用是由电话费和上网费两部分组成,过去,某市网民通过电脑拨号上“因特网”的费用为电话费每3分钟0.18元,上网费每小时7.2元,现在,该市对上“因特网”的费用作了调整:电话费每3分钟0.22元,上网费为每月不超过60小时,按每小时4元计算;超过60小时部分,按每小时8元计算.
(1)根据调整后的规定,用解析式表示网民每月上“因特网”的费用![]() (元)与上网时间
(元)与上网时间![]() 之间的函数关系式;
之间的函数关系式;
(2)资费调整前,网民小刚在其家庭经济预算中,一直有一笔每月70小时的上网费用支出,因“因特网”资费调整后,小刚要想不超过其家庭经济预算中的上网费用支出,他现在每月至多可上网多少小时?
(3)从资费调整前后该市网民上网费用的支出增减情况分析,哪些网民支出增加?哪些网民支出减少?
参考答案:
【答案】(1)y=![]() ;(2)至多可上网约80.32h;(3)当上网时间小于150时,调整后需费用少;当等于150时,调整前后所需费用相同;当大于150时,调整前所需费用少.
;(2)至多可上网约80.32h;(3)当上网时间小于150时,调整后需费用少;当等于150时,调整前后所需费用相同;当大于150时,调整前所需费用少.
【解析】
(1)对于第一问,根据已知调整后“因特网”的费用调整为电话0.22元/3min,上网费为每月不超过60h,按4元/h计算;可以得出调整后的电话费为0.22*20=4.4(元/时);再结合上网费用=网费电话费,网费不超过60h,为4元/h,即每小时上网所花费用8.4,网费超过60h,为8元/h,即超时每小时为12.4,即可解答;
(2)由已知条件网民晓刚在其家庭经济预算中,一直有一笔每月70h的上网费用支出,可以得出上网70h所需的费用为(3.6+7.2)×70=756(元);资费调整后,若上网60h,则所需费用为8.4×60=504(元,因为756>504,所以晓刚现在上网时间超过60h,得出关系式12.4(x-60)+504≤756,即可解答.
(3)先设出未知数调整前所需费用y![]() 元,调整后所需费用为y
元,调整后所需费用为y![]() 元,然后分情况讨论,得出解答结果.
元,然后分情况讨论,得出解答结果.
(1)由题意知调整后每小时的电话费为:0.22×20=4.4(元/时)
根据上网费用=网费电话费,网费不超过60h,为4元/h,即每小时上网所花费用8.4元
若网费,超过60h,为8元/h,即超时时每小时的上网费用为12.4元
所以设上网时间为x,与费用y的函数关系式为
y=![]()
(2)资费调整前,上网70h所需的费用为(3.6+7.2)×70=756(元)
资费调整后,若上网60h,则所需费用为:8.4×60=504(元)
因为756>504,
所以晓刚现在上网时间超过60h,
由12.4(x-60)+504≤756,
解得:x≤80.32h.
所以小刚现在每月至多可上网约80.32h.
(3)设调整前所需费用y![]() 元,调整后所需费用为y
元,调整后所需费用为y![]() 元.则y
元.则y![]() =10.8x
=10.8x
当0≤x≤60时,
y![]() =8.4x,
=8.4x,
由10.8x>8.4x,
故y![]() >y
>y![]() ,
,
当x>60,y![]() =12.4x240,
=12.4x240,
当y![]() =y
=y![]() 时,
时,
10.8x=12.4x-240,
解得:x=150,
当y![]() >y
>y![]() 时,
时,
10.8x>12.4x-240,
解得:x<150,
当y![]() <y
<y![]() 时,
时,
10.8x<12.4x-240,
解得:x>150,
当上网时间小于150时,调整后需费用少;
当等于150时,调整前后所需费用相同;
当大于150时,调整前所需费用少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】季末打折促销,甲乙两商场促销方式不同,两商场实际付费
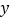 (元)与标价
(元)与标价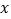 (元)之间的函数关系如图所示折线
(元)之间的函数关系如图所示折线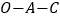 (虚线)表示甲商场,折线
(虚线)表示甲商场,折线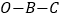 表示乙商场
表示乙商场(1)分别求射线
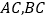 的解析式.
的解析式.(2)张华说他必须选择乙商场,由此推理张华计划购物所需费用
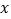 (元)(标价)的范围是______.
(元)(标价)的范围是______.(3)李明说他必须选择甲商场,由此推理李明计划购物所需费用
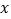 (元)(标价)的范围是______.
(元)(标价)的范围是______.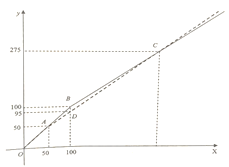
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车往返于甲、乙两地之间,如果汽车以50千米/时的平均速度从甲地出发,则6小时可到达乙地.
(1)写出时间t(时)关于速度v(千米/时)的函数关系式,并画出函数图象.
(2)若这辆汽车需在5小时内从甲地到乙地,则此时汽车的平均速度至少应是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
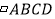 ,顶点
,顶点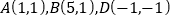 ;直线
;直线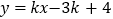 .
.(1)点
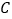 的坐标是______,对角线
的坐标是______,对角线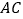 与
与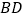 的交点
的交点 的坐标是______.
的坐标是______.(2)①过点
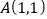 的直线
的直线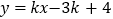 的解析式是______.
的解析式是______.②过点
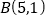 的直线
的直线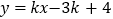 的解析式是______.
的解析式是______.③判断①、②中两条直线的位置关系是______.
(3)当直线
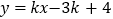 平分
平分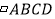 的面积时,
的面积时,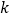 的值是______.
的值是______.(4)一次函数
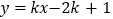 的图像______(填“能”或“不能”)平分
的图像______(填“能”或“不能”)平分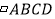 的面积.
的面积.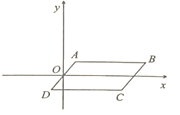
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 ,
, ,
, ,
, ,
, 在同一条直线上,
在同一条直线上, ,
, 为
为 的中点,
的中点, .
.
(1)图中共有直线______条,线段______条,射线______条;
(2)求线段
 的长度.
的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)如图①,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为 .
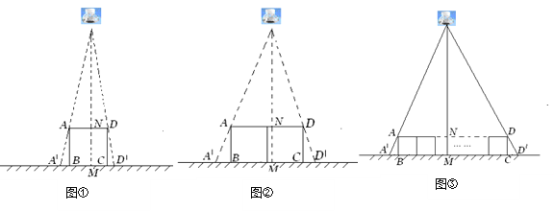 (2)不改变①中灯泡的高度,将两个边长为30cm的正方形框架按图②摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(2)不改变①中灯泡的高度,将两个边长为30cm的正方形框架按图②摆放,请计算此时横向影子A′B,D′C的长度和为多少?(3)有n个边长为a的正方形按图③摆放,测得横向影子A′B,D′C的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
-
科目: 来源: 题型:
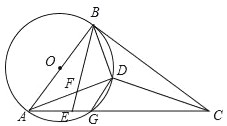
查看答案和解析>>【题目】如图:AB是⊙O的直径,AC交⊙O于G,E是AG上一点,D为△BCE内心,BE交AD于F,且∠DBE=∠BAD.
(1)求证:BC是⊙O的切线;
(2)求证:DF=DG;
(3)若∠ADG=45°,DF=1,则有两个结论:①ADBD的值不变;②AD-BD的值不变,其中有且只有一个结论正确,请选择正确的结论,证明并求其值.
相关试题

