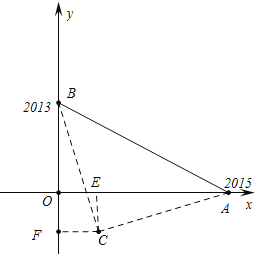
【题目】已知,在平面直角坐标系中,点A(2015,0)、B(0,2013),以AB为斜边在直线AB下方作等腰直角△ABC,则点C的坐标为 .
参考答案:
【答案】(1,﹣1).
【解析】
试题分析:如图设△CAB是等腰直角三角形,点C坐标(x,y),作CE⊥OA于E,CF⊥OB于F,先证明△ACE≌△BCF,推出四边形OECF是正方形,列出方程即可解决问题.
解:如图设△CAB是等腰直角三角形,点C坐标(x,y),作CE⊥OA于E,CF⊥OB于F.
∵∠CEO=∠CFO=∠EOF=90°.
∴四边形OECF是矩形,
∴CE=OF,PF=OE,∠ECF=90°,
∵∠ECF=∠ACB=90°,
∴∠ACE=∠BCF,
在△ACE和△BCF中,
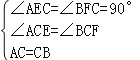 ,
,
∴△ACE≌△BCF,
∴CE=CF,AE=BF,
∴四边形OECF是正方形,
∴x=﹣y,2013+x=2015﹣x,
∴x=1,y=﹣1,
∴点C坐标(1,﹣1).
故答案为(1,﹣1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多项式是三次二项式,则这个多项式可以是( )
A.x2﹣2x+1 B.2x3+1 C.x2﹣2x D.x3﹣2x2+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】冬季某天我国三个城市的最高气温分别是﹣10℃,1℃,﹣7℃,它们任意两城市中最大的温差是( )
A. 11℃ B. 17℃ C. 8℃ D. 3℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆锥的底面半径为9cm,母线长为10cm,则圆锥的全面积是 cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】书店举行购书优惠活动:
①一次性购书不超过100元,不享受打折优惠;
②一次性购书超过100元但不超过200元一律打九折;
③一次性购书200元一律打七折.
小丽在这次活动中,两次购书总共付款229.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是 元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB:y=﹣
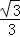 x+
x+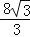 交坐标轴于A、B两点,直线AC与AB关于y轴对称,交x轴于点C.点P、Q分别是线段BC、AC上两个动点,且∠APQ始终等于30°.
交坐标轴于A、B两点,直线AC与AB关于y轴对称,交x轴于点C.点P、Q分别是线段BC、AC上两个动点,且∠APQ始终等于30°.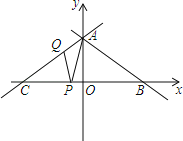
(1)点B的坐标是( , );∠ABC= 度;
(2)若⊙O与AB相切,则⊙O的半径等于 ;
(3)当P点坐标为(﹣2,0)时,求CQ的长;
(4)当△APQ为等腰三角形时,求P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请写出“对顶角相等”的逆命题:______.
相关试题

