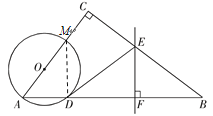
【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长.

参考答案:
【答案】(1)直线DE与⊙O相切;(2)4.75.
【解析】试题分析:(1) 直线DE与⊙O相切,连接OD,根据等腰三角形的性质可得∠A=∠ODA,根据线段垂直平分线的性质及等腰三角形的性质易得∠B=∠EDB,易证ODA+∠EDB=![]() ,即可得∠ODE=
,即可得∠ODE=![]() -
-![]() =
=![]() ,所以直线DE与⊙O相切;(2)连接OE,设DE=x,则EB=ED=x,CE=8-x.因∠C=∠ODE =
,所以直线DE与⊙O相切;(2)连接OE,设DE=x,则EB=ED=x,CE=8-x.因∠C=∠ODE =![]() ,根据勾股定理可得
,根据勾股定理可得![]() ,即
,即![]() ,解得x的值即可得线段DE的长.
,解得x的值即可得线段DE的长.
试题解析: (1) 直线DE与⊙O相切.
理由如下:
连接OD,
∵OD=OA,
∴∠A=∠ODA.
∵EF是BD的垂直平分线,
∴EB="ED."
∴∠B=∠EDB.
∵∠C=![]() ,
,
∴∠A+∠B=![]() .
.
∴∠ODA+∠EDB=![]() .
.
∴∠ODE=![]() -
-![]() =
=![]() .
.
∴直线DE与⊙O相切.
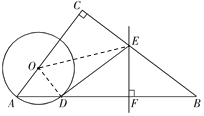
(2) 解法一:
连接OE,
设DE=x,则EB=ED=x,CE=8-x.
∵∠C=∠ODE =![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
即DE=![]() .
.
解法二:
连接DM,
∵AM是直径,
∴∠MDA=![]() ,AM=4.
,AM=4.
又∵∠C=![]() ,
,
∴![]() ,
,
![]() .
.
∴![]() , ∴AD=2.4.
, ∴AD=2.4.
∴BD=10-2.4=7.6.
∴BF=![]() .
.
∵EF⊥BD,∠C=![]() ,
,
∴![]() .
.
∴![]() , BE=
, BE=![]() .
.
∴DE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB∥x轴,且AB=3,若点A的坐标是(﹣1,2),则B点的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直线y=-6x向上平移5个单位长度,所得直线的函数解析式是y=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在抗击新冠状病毒战斗中,有152箱公共卫生防护用品要运到A、B两城镇,若用大小货车共15辆,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,则恰好能一次性运完这批防护用品求这大小货车各多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定,“中小学生每天在校体育锻炼时间不小于
 小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:
小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况: 组:时间小于
组:时间小于 小时;
小时; 组:时间大于等于
组:时间大于等于 小时且小于
小时且小于 小时;
小时; 组:时间大于等于
组:时间大于等于 小时且小于
小时且小于 小时;
小时; 组:时间大于等于
组:时间大于等于 小时.
小时.

根据以上信息,回答下列问题:
(
 )补全条形统计图和扇形统计图.
)补全条形统计图和扇形统计图.(
 )本次调查数据的中位数落在__________组.
)本次调查数据的中位数落在__________组.(
 )根据统计数据估计该地区
)根据统计数据估计该地区 名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有多少人?
名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车
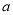 辆,B型车
辆,B型车 辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=
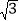 x+1的图象分别与x轴、y轴交于A、B两点,以A为圆心,适当长为半径画弧分别交AB、AO于点C、D,再分别以C、D为圆心,大于
x+1的图象分别与x轴、y轴交于A、B两点,以A为圆心,适当长为半径画弧分别交AB、AO于点C、D,再分别以C、D为圆心,大于 CD的长为半径画弧,两弧交于点E,连接AE并延长交y轴于点F,则下列说法正确的个数是( )
CD的长为半径画弧,两弧交于点E,连接AE并延长交y轴于点F,则下列说法正确的个数是( )①AF是∠BAO的平分线;
②∠BAO=60°;
③点F在线段AB的垂直平分线上;
④S△AOF:S△ABF=1:2.

A. 1 B. 2 C. 3 D. 4
相关试题

