【题目】如图,已知直线y=3x+3与x轴交于点A,与x轴交于点B,过A,B两点的抛物线交x轴于另一点C(3,0).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△ABP是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,说明理由.

参考答案:
【答案】(1)y=﹣x2+2x+3(2)(1,![]() )、(1,﹣
)、(1,﹣![]() )、(1,0)或(1,1)
)、(1,0)或(1,1)
【解析】
试题分析:(1)设抛物线的解析式为y=ax2+bx+c.由一次函数的解析式可求出点A、B的坐标,再结合点A、B、C三点的坐标利用待定系数法即可求出抛物线的解析式;
(2)假设存在,根据抛物线的解析式找出抛物线的对称轴,设出点P的坐标,利用两点间的距离找出线段PA、PB和AB的长度,分三种情况讨论△ABP为等腰三角形,根据等腰三角形的性质找出两边相等,从而找出关于m的一元二次方程,解方程求出m值,从而即可得出点P的坐标.
试题解析:(1)设抛物线的解析式为y=ax2+bx+c.
∵直线y=3x+3交x轴于点A,交y轴于点B,
∴A(﹣1,0),B(0,3).
又抛物线经过A,B,C三点,
∴根据题意,得: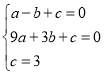 ,
,
解得: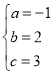 ,
,
∴抛物线的解析式为y=﹣x2+2x+3.
(2)假设存在.
∵抛物线的解析式为y=﹣x2+2x+3,
∴该抛物线的对称轴为x=1.
设点P的坐标为(1,m),又A(﹣1,0),B(0,3),
则AP=![]() ,
,
BP=![]() ,
,
AB=![]() .
.
△ABP是等腰三角形分三种情况:
①当AB=AP时,![]() ,
,
解得:m1=![]() ,m2=﹣
,m2=﹣![]() ,
,
∴点P的坐标为(1,![]() )或(1,﹣
)或(1,﹣![]() );
);
②当AB=BP时,![]() ,
,
解得:m3=0,m4=6(A、B、P三点共线,舍去),
∴点P的坐标为(1,0);
③当AP=BP时,![]() ,
,
解得:m5=m6=1,
∴点P的坐标为(1,1).
综上可得:在抛物线的对称轴上存在点P,使△ABP是等腰三角形,此时点P的坐标为(1,![]() )、(1,﹣
)、(1,﹣![]() )、(1,0)或(1,1).
)、(1,0)或(1,1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,∠B=∠C=90 ,M是BC的中点,DM平分∠ADC.
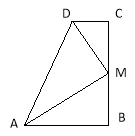
(1)若连接AM,则AM是否平分∠BAD?请你证明你的结论;
(2)线段DM与AM有怎样的位置关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 中,BD、CE分别是AC、AB上的高,BD与CE交于点O.BE=CD

(1)问△ABC为等腰三角形吗?为什么?
(2)问点O在∠A的平分线上吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD在直角坐标系内,点A(0,1),点B(0,0),则点C,D坐标分别为______和______.(只写一组)
-
科目: 来源: 题型:
查看答案和解析>>【题目】据统计,今年春节期间(除夕到初五),微信红包总收发次数达321亿次,几乎覆盖了全国75%的网民,数据“321亿”用科学记数法可表示为( )
A.3.21×108
B.321×108
C.321×109
D.3.21×1010 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点(2,﹣1)关于原点对称的点的坐标是 _________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?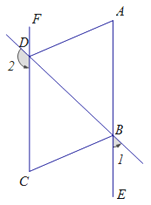
相关试题

