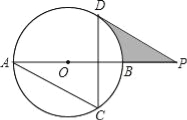
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
参考答案:
【答案】(1)证明见解析;(2)![]() cm2
cm2
【解析】
试题分析:(1)连接OD,求出∠AOD,求出∠DOB,求出∠ODP,根据切线判定推出即可;
(2)求出OP、DP长,分别求出扇形DOB和三角形ODP面积,即可求出答案.
试题解析:(1)连接OD,

∵∠ACD=60°,
∴由圆周角定理得:∠AOD=2∠ACD=120°,
∴∠DOP=180°﹣120°=60°,
∵∠APD=30°,
∴∠ODP=180°﹣30°﹣60°=90°,
∴OD⊥DP,
∵OD为半径,
∴DP是⊙O切线;
(2)∵∠P=30°,∠ODP=90°,OD=3cm,
∴OP=6cm,由勾股定理得:DP=3![]() cm,
cm,
∴图中阴影部分的面积S=S△ODP﹣S扇形DOB=![]() ×3×3
×3×3![]() ﹣
﹣![]() cm2
cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:3ab+6a=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式5x2+4x﹣x3﹣3按x的降幂排列为_____.
-
科目: 来源: 题型:
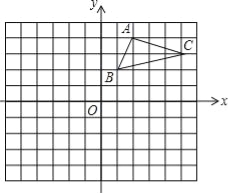
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
-
科目: 来源: 题型:
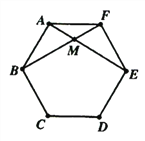
查看答案和解析>>【题目】如图,正六边形ABCDEF的对角线AE与BF相交于点M.
(1)求证:△ABM≌△FEM;
(2)已知AM=2,求BF的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:7a2b+(﹣4a2b+5ab2)﹣2(2a2b﹣3ab2),其中(a﹣2)2+|b+
 |=0.
|=0.
相关试题

