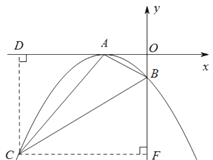
【题目】如图,已知抛物线y=ax2+bx+c的顶点A在x轴上,与y轴的交点B(0,-1),且b=-4ac。
(1)求点A的坐标;
(2)求抛物线的解析式
(3)在抛物线上是否存在一点C,使以BC为直径的圆经过抛物线的顶点A?若不存在请说明理由;若存在,求出点C的坐标,并求出此时圆的圆心点P的坐标。

参考答案:
【答案】(1)A(-2,0);(2)![]() =-
=-![]() -
-![]() -1;(3)点C存在,点C的坐标为(-10,-16)或(-2,0),点P的坐标为(-5,-
-1;(3)点C存在,点C的坐标为(-10,-16)或(-2,0),点P的坐标为(-5,- ![]() )或(-1,-
)或(-1,- ![]() ).
).
【解析】试题分析:
(1)把点B(0,-1)代入解析式可解得: ![]() ,代入
,代入![]() 可得
可得![]() ,由点A是抛物线顶点,∴其横坐标为
,由点A是抛物线顶点,∴其横坐标为![]() ,再由点A在横轴上得到其坐标为:
,再由点A在横轴上得到其坐标为: ![]() ;
;
(2)把点A![]() 代入解析式
代入解析式![]() 可得:
可得: ![]() ,结合(1)中得到的
,结合(1)中得到的![]() 可解得
可解得![]() ,从而可得到解析式为
,从而可得到解析式为![]() ;
;
(3)如图,由题意可设符合条件的点C的坐标为![]() ,作CD⊥x轴于点D,CF⊥y轴于点F,然后可在Rt△ADC、Rt△BCF和Rt△AOB中利用勾股定理把AC2、BC2和AB2分别用含“x”的式子表达出来;由点A在以BC为直径的圆上,可得∠BAC=90°,从而可由勾股定理建立方程解出“x”的值,就可得到点C的坐标了,最后利用线段的中点坐标公式就可以求出圆心P的坐标.
,作CD⊥x轴于点D,CF⊥y轴于点F,然后可在Rt△ADC、Rt△BCF和Rt△AOB中利用勾股定理把AC2、BC2和AB2分别用含“x”的式子表达出来;由点A在以BC为直径的圆上,可得∠BAC=90°,从而可由勾股定理建立方程解出“x”的值,就可得到点C的坐标了,最后利用线段的中点坐标公式就可以求出圆心P的坐标.
试题解析:
(1)把B(0,-1)坐标
代入![]() =
=![]() +
+![]() +
+![]() 中,得
中,得![]() =-1,
=-1,
由![]() =-4
=-4![]() ,得
,得![]() =4
=4![]() ,
,
∵A为抛物线的顶点,∴其横坐标为![]() =-
=-![]() ,
,
∴![]() =-2,即点A的坐标为A(-2,0);
=-2,即点A的坐标为A(-2,0);
(2)把点A的坐标(-2,0)代入抛物线解析式中,
可得![]() ,
,
把![]() =4
=4![]() 代入上式,得
代入上式,得![]() =-
=-![]() ,
,
∴![]() =-1,
=-1,
∴抛物线的解析式为: ![]() =-
=-![]() -
-![]() -1;
-1;
(3)点C存在.
设符合题意的点C坐标为![]() ,过点C作CD⊥x轴于点D,作CF⊥y轴于点F,则在Rt△ADC、Rt△BCF和Rt△AOB中,由勾股定理分别可得:
,过点C作CD⊥x轴于点D,作CF⊥y轴于点F,则在Rt△ADC、Rt△BCF和Rt△AOB中,由勾股定理分别可得: ![]() ,
, ![]() ,
, 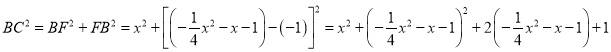 ∵点A在以BC为直径的圆上,
∵点A在以BC为直径的圆上,
∴∠BAC=90°,
∴![]() ,
,
即: ![]() =5+
=5+![]() ,
,
解得: ![]() ,
,
∴ C的坐标为![]() 或
或![]() ;
;
因为点P是以BC为直径的圆的圆心,点B的坐标为![]() ,
,
∴由线段中点坐标公式可得:①当点C的坐标为![]() 时,点P的坐标为:
时,点P的坐标为: ![]() ;②当点C的坐标为
;②当点C的坐标为![]() 时,点P的坐标为:
时,点P的坐标为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中,放有四张质地完全相同的卡片,分别标有数字1,2,3,4.第一次从袋中随机地抽出一张卡片,把其上的数字记为横坐标x,然后把卡片放回袋中,搅匀后第二次再随机地从中抽出一张,把其上的数字记为纵坐标y.
(1)用树状图或列表法把所有可能的点表示出来;
(2)求所得的点在直线y=﹣x+5的点的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面上,正方形ABCD的四个顶点到直线l的距离只取四个值,其中一个值是另一个值的3倍,这样的直线l可以有( )
A. 4条 B. 8条 C. 12条 D. 16条
-
科目: 来源: 题型:
查看答案和解析>>【题目】搬进新居后,小杰自己动手用彩塑纸做了一个如图所示的正方形的挂式小饰品ABCD,彩线BD.AN.CM将正方形ABCD分成六部分,其中M是AB的中点,N是BC的中点,AN与CM交于O点.已知正方形ABCD的面积为576cm2,则被分隔开的△CON的面积为( )

A. 96cm2 B. 48cm2 C. 24cm2 D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】4是的算术平方根.
-
科目: 来源: 题型:
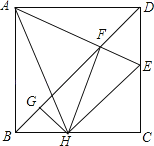
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=4,E为CD上一动点,AE交BD于F,过F作FH⊥AE于H,过H作GH⊥BD于G,下列有四个结论:①AF=FH,②∠HAE=45°,③BD=2FG,④△CEH的周长为定值,其中正确的结论有( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有( )
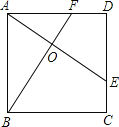
A.1个 B.2个 C.3个 D.4个
相关试题

