Question

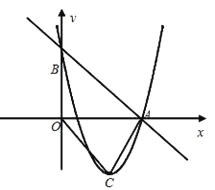
【题目】如图，在直角坐标平面内，直线y=－x+5与轴和轴分别交于A、B两点，二次函数y=+bx+c的图象经过点A、B，且顶点为C．

（1）求这个二次函数的解析式；

（2）求sin∠OCA的值；

（3）若P是这个二次函数图象上位于x轴下方的一点，且ABP的面积为10，求点P的坐标．

Answer 1

【答案】（1）、；（2）、；（3）、P（4，－3）.

【解析】试题分析：（1）、根据一次函数求出A、B两点的坐标，然后代入反比例解析式进行求解；（2）、过点C作CH⊥x轴，求出CH、AH、AC、OC、OA的长度，将∠OAC转化成∠OCA，然后进行计算；（3）、过点P作PQ⊥x轴并延长角直线于点Q，设出点P和点Q的坐标，求出PQ的长度，根据三角形的面积关系列出方程，然后进行求解，根据点P在x轴下方进行舍根.

试题解析：（1）、由直线y=－x+5得点B（0，5），A（5，0），将A、B两点的坐标代入，

得，解得∴抛物线的解析式为

（2）、过点C作CH⊥x轴交x轴于点H 把配方得∴点C（3，-4），

∴CH=4，AH=2，AC=∴OC=5， ∵OA=5 ∴OA=OC ∴∠OAC=∠OCA

sin∠OCA=sin∠OAC=

（3）、过P点作PQx轴并延长交直线y=－x+5于Q

设点P（m， －6m+5），Q（m,-m+5） ∴PQ=－m+5－（－6m+5）=－+5m

∵

∴

∴∴

∴P（1,0）（舍去），P（4，-3）