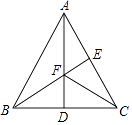
【题目】如图，等边△ABC中，AB=4，E是线段AC上的任意一点，∠BAC的平分线交BC于D，AD=2 
，F是AD上的动点，连接CF、EF，则CF+EF的最小值为 ． 
【答案】2 
【解析】解：∵AD是等边△ABC的∠BAC的平分线，∴AD⊥BC，BD=CD，
∴点B、C关于AD对称，
过点B作BE⊥AC于E，交AD于F，连接CF，
由轴对称确定最短路线问题，点E、F即为使CF+EF的最小值的点，
∵△ABC是等边三角形，AD、BE都是高，
∴BE=AD=2 ，
∴CF+EF的最小值=BE=2 ．
所以答案是：2 ．
【考点精析】通过灵活运用等边三角形的性质和轴对称-最短路线问题，掌握等边三角形的三个角都相等并且每个角都是60°；已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径即可以解答此题．
科目：初中数学 来源： 题型：
【题目】如图，射线
上有三点
、
、
，满足
， 
， 
，点
从点
出发，沿
方向以
秒的速度匀速运动，点
从点
出发在线段
上向点
匀速运动，两点同时出发，当点
运动到点
时，点
、
停止运动.
(1)若点
运动速度为
秒，经过多长时间
、
两点相遇?
(2)当
在线段
上且
时，点
运动到的位置恰好是线段
的三等分点，
求点
的运动速度;
(3)当点
运动到线段
上时，分别取
和
的中点
、
，求
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市居民生活用电基本价格为每千瓦时0.60元，若每月用电量超过70千瓦时，超出部分按照基本电价的120%收费．
（1）若小明家用电量用a表示，请用代数式分别表示出用电量不超过70千瓦时和超过70千瓦时的收费标准．
（2）若该户居民8月份用电量为100千瓦时，则应收费多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线 l 与 x 轴， y 轴分别交于 M，N 两点，且 OM=ON=3．
（1）求这条直线的函数表达式；
（2）Rt△ ABC 与直线 l 在同一个平面直角坐标系内，其中∠ABC=90°，AC= 2
，A（1，0），B（3，0），将△ABC 沿 x 轴向左平移，当点 C 落在直线 l 上时，求线段 AC 扫过的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明用的练习本可以到甲商店购买，也可以到乙商店购买，已知两商店的标价都是每本1元，甲商店的优惠条件是：购买10本以上，从第11本开始按标价的70%卖；乙商店的优惠条件是：从第一本按标价的80%卖.
（1）小明要买20本时，到哪个商店较省钱？
（2）买多少本时给两个商店付相等的钱？
（3）小明现有40元钱，最多可买多少本？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
