【题目】如图,等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 是斜边
是斜边![]() 上的一点,将
上的一点,将![]() 沿
沿![]() 翻折得
翻折得![]() ,连接
,连接![]() ,若
,若![]() 是等腰三角形,则
是等腰三角形,则![]() 的长是______.
的长是______.

参考答案:
【答案】![]() 或
或![]()
【解析】
分两种情形:①如图1中,当ED=EA时,作DH⊥BC于H.②如图2中,当AD=AE时,分别求解.
如图1中,当ED=EA时,作DH⊥BC于H.
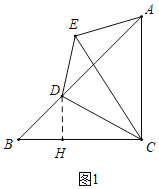
∵CB=CA,∠ACB=90°,
∴∠B=∠CAB=45°,
由翻折不变性可知:∠CED=∠B=45°,
∴A,C,D,E四点共圆,
∵ED=EA,
∴∠ACE=∠ECD=∠BCD=30°,设BH=DH=x,则CH=![]() x,
x,
∵BC=![]() ,
,
∴x+![]() x=
x=![]() ,
,
∴x=![]() .
.
∴BD=![]() x=
x=![]() -1.
-1.
如图2中,当AD=AE时,同法可证:∠ACD=∠ACE,
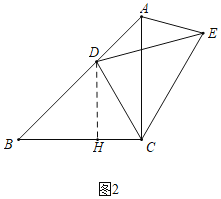
∵∠BCD=∠DCE,
∴∠BCD=2∠ACD,
∴∠BCD=60°,设BH=DH=x,则CH=![]() x,
x,
∵BC=![]() ,
,
∴x+![]() x=
x=![]() ,
,
∴x=![]() ,
,
∴BD=![]() x=3-
x=3-![]() .
.
综上所述,满足条件的BD的值为![]() -1或3-
-1或3-![]() .
.
故答案为:![]() -1或3-
-1或3-![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】缴纳个人所得税是收入达到缴纳标准的公民应居的义务,个人所得税率是由国家相应的法律法规规定的.根据个人的收入计算,新修改的《中华人民共和国个人所得税法》于2019年1月1日正式实施,新税法规定个人所得税的免征额为5000元,应纳税所得额按如下税率表缴纳个人所得税(应纳税所得额=税前收总额﹣国家规定扣除专项金额﹣免征额).
级数
应纳税所得额
税率%
1
不超过3000元的
3
2
超过3000元至12000元的部分
10
3
超过12000元至25000元的部分
20
…
…
…
根据以上信息,解决以下问题:
(1)小明的妈妈应纳税所得额为2000元,她应该缴纳个人所得税______元.
(2)小明的爸爸要缴纳个人所得税590元,他应纳税所得额是多少元?
(3)如果小明的爸爸和妈妈某月应纳税所得额共为20000元(爸爸的应纳税所得额高于妈妈的应纳税所得额),共要缴纳个人所得税1780元,小明的爸爸应纳税所得额是_____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮家与姥姥家相距24km. 小亮8:00从家出发,骑自行车去姥姥家,妈妈8:30从家出发,乘车沿相同路线去姥姥家. 在同一直角坐标系中,小亮和妈妈的行进路程S(km)与北京时间t(时)的函数图象如图所示. 根据图象得到下列结论,其中错误的是( )

A. 小亮骑自行车的平均速度是12km/h
B. 妈妈比小亮提前0.5小时到达姥姥家
C. 妈妈在距家12km处追上小亮
D. 9:30妈妈追上小亮
-
科目: 来源: 题型:
查看答案和解析>>【题目】若从 -3,-1,0,1,3这五个数中随机抽取一个数记为a,再从剩下的四个数中任意抽取一个数记为b,恰好使关于x,y的二元一次方程组
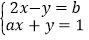 有整数解,且点(a,b)落在双曲线
有整数解,且点(a,b)落在双曲线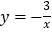 上的概率是_________.
上的概率是_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOD=160°,OB、OC、OM、ON是∠AOD内的射线.
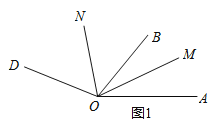
(1)如图1,若OM平分∠AOB,ON平分∠BOD.当OB绕点O在∠AOD内旋转时,求∠MON的大小;
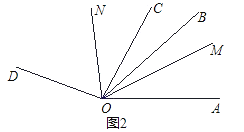
(2)如图2,若∠BOC=20°,OM平分∠AOC,ON平分∠BOD.当∠BOC绕点O在∠AOD内旋转时,求∠MON的大小;
(3)在(2)的条件下,若∠AOB=10°,当∠B0C在∠AOD内绕着点O以2度/秒的速度逆时针旋转t秒时,∠AOM=
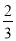 ∠DON.求t的值.
∠DON.求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】小华将一条直角边长为1的一个等腰直角三角形纸片(如图1),沿它的对称轴折叠1次后得到一个等腰直角三角形(如图2),再将图2的等腰直角三角形沿它的对称轴折叠后得到一个等腰直角三角形(如图3),则图3中的等腰直角三角形的一条腰长为_________;同上操作,若小华连续将图1的等腰直角三角形折叠n次后所得到的等腰直角三角形(如图n+1)的一腰长为_________.
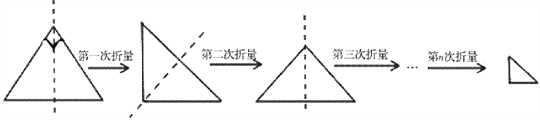
图1 图2 图3 图n+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城镇在对一项工程招标时,接到甲、乙两个工程队的投标书,每施工一天,需付甲队工程款2万元,付乙队工程款1.5万元.现有三种施工方案:(
 )由甲队单独完成这项工程,恰好如期完工;(
)由甲队单独完成这项工程,恰好如期完工;( )由乙队单独完成这项工程,比规定工期多6天;(
)由乙队单独完成这项工程,比规定工期多6天;( )由甲乙两队
)由甲乙两队 后,剩下的由乙队单独做,也正好能如期完工.小聪同学设规定工期为
后,剩下的由乙队单独做,也正好能如期完工.小聪同学设规定工期为 天,依题意列出方程:
天,依题意列出方程: .
.(1)请将(
 )中被墨水污染的部分补充出来:________;
)中被墨水污染的部分补充出来:________;(2)你认为三种施工方案中,哪种方案既能如期完工,又节省工程款?说明你的理由.
相关试题

