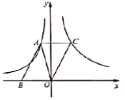
【题目】如图,在平而直角坐标系![]() 中,函数
中,函数![]() (其中
(其中![]() ,
,![]() )的图象经过平行四边形
)的图象经过平行四边形![]() 的顶点
的顶点![]() ,函数
,函数![]() (其中
(其中![]() )的图象经过顶点
)的图象经过顶点![]() ,点
,点![]() 在
在![]() 轴上,若点
轴上,若点![]() 的横坐标为1,
的横坐标为1,![]() 的面积为
的面积为![]() .
.
(1)求![]() 的值:
的值:
(2)求直线![]() 的解析式.
的解析式.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设![]() 与
与![]() 轴相交于点
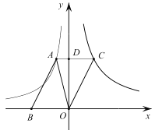
轴相交于点![]() ,根据已知求出点C的坐标,利用平行四边形的性质证得OD=2,CD=1,再根据
,根据已知求出点C的坐标,利用平行四边形的性质证得OD=2,CD=1,再根据![]() 的面积为
的面积为![]() 求出AD即可求出得到点A的坐标求出k;
求出AD即可求出得到点A的坐标求出k;
(2)根据平行四边形的性质求出点B的坐标,再设直线![]() 的解析式为
的解析式为![]() ,将点A、B的坐标代入解答即可.
,将点A、B的坐标代入解答即可.
(1)解:设![]() 与
与![]() 轴相交于点
轴相交于点![]() .
.
把![]() 代入
代入![]() ,得
,得![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() .
.
![]() .
.
![]() ,
,![]() .
.
根据题意,得![]() .
.
![]() .
.
![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
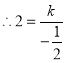 .
.
解得![]() .
.
(2)![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,
,
∴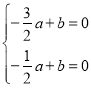 ,解得
,解得![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.

