【题目】如图,在Rt△ABC中,∠C=90°,AC=10,BC=8,AB的垂直平分线分别交AC、AB于点D、E.则AD的长度为 . 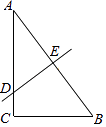
参考答案:
【答案】8.2
【解析】解:连接BD,如图所示: 
∵DE是线段AB的垂直平分线,
∴AD=BD,
设AD=BD=x,
则CD=AC﹣AD=10﹣x,
在Rt△BCD中,由勾股定理得:82+(10﹣x)2=x2 ,
解得:x=8.2;
所以答案是:8.2.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图案中,是轴对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的是一个正方体纸盒的展开图,按虚线折成正方体后,若使相对面上的两数互为相反数,试写出A,B,C分别表示的数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )
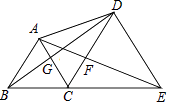
A.△ACE≌△BCD
B.△BGC≌△AFC
C.△ADB≌△CEA
D.△DCG≌△ECF -
科目: 来源: 题型:
查看答案和解析>>【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=
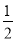 ,tanβ=
,tanβ=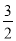 ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系.(1)求点P的坐标;
(2)水面上升1m,水面宽多少(
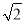 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?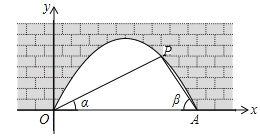
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣22+2cos60°+(π﹣3.14)0+(﹣1)2018
-
科目: 来源: 题型:
查看答案和解析>>【题目】实数a,b,c在数轴上的位置如图所示.
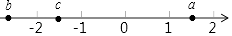
(1)比较大小:|a|与|b|.
(2)化简:|c|﹣|a|+|﹣b|+|﹣a|.
相关试题

