【题目】在综合与实践课上老师将直尺摆放在三角板上,使直尺与三角板的边分别交于点P、M、N、Q,
(1)如图①所示.当∠CNG=42°,求∠HMC 的度数.(写出证明过程)
(2)将直尺向下平移至图 2 位置,使直尺的边缘通过点 C,交 AB 于点 P,直尺另一侧与三角形交于 N、Q 两点。请直接写出∠PQF、∠A、∠ACE 之间的关系.

参考答案:
【答案】(1)48°;(2)∠PQF=∠A+∠ACE,理由见解析
【解析】
(1)过点C作CD∥EH,根据两直线平行,内错角相等可得∠DCN=∠CNG=42°,进而可证得∠HMC=∠ACD=48°即可;
(2)根据平行线的性质及三角形的外角性质即可得证.
解:(1)如图,过点C作CD∥EH,
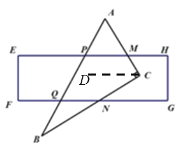
∵CD∥EH,EH∥FG,
∴CD∥FG,
∴∠DCN=∠CNG=42°,
∵∠ACB=90°,
∴∠ACD=∠ACB﹣∠DCN=90°﹣42°=48°,
∵CD∥EH,
∴∠HMC=∠ACD=48°,
(2)∠PQF=∠A+∠ACE,理由如下:
∵EH∥FG,
∴∠PQF=∠APE,
∵∠APE是△APM的外角,
∴∠APE=∠A+∠ACE,
∴∠PQF=∠A+∠ACE.
-
科目: 来源: 题型:
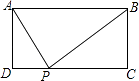
查看答案和解析>>【题目】如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP= .
-
科目: 来源: 题型:
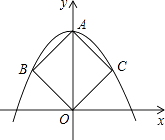
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数y=ax2+c(a≠0)的图象过正方形ABOC的三个顶点A,B,C,则ac的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A城气象台测得台风中心在A城正西方向600km的B处,以每小时200km的速度向北偏东60°的方向移动,距台风中心500km的范围内是受台风影响的区域.

(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风的影响,那么A城遭受这次台风影响有多长时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC边上的动点,点P从点A开始沿AB方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t秒.
(1)出发2秒后,求PQ的长;
(2)从出发几秒钟后,△PQB能形成等腰三角形?
(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
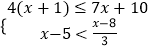 ,并写出它的所有非负整数解.
,并写出它的所有非负整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程
(1)3x﹣1=2﹣x (2)
 ﹣
﹣ =1
=1(3)
 (4)
(4)
相关试题

