【题目】如图,抛物线![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,直线
,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,将直线
,将直线![]() 向上平移后得到直线
向上平移后得到直线![]() ,直线
,直线![]() 刚好经过抛物线与
刚好经过抛物线与![]() 轴正半轴的交点
轴正半轴的交点![]() 和与
和与![]() 轴的交点
轴的交点![]() .
.

(1)直接写出点![]() 和点
和点![]() 的坐标,并求出点
的坐标,并求出点![]() 的坐标;
的坐标;
(2)若点![]() 是抛物线第一象限内的一个动点,连接
是抛物线第一象限内的一个动点,连接![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() 和
和![]() .设
.设![]() 的面积为
的面积为![]() ,当
,当![]() 取得最大值时,求出此时点
取得最大值时,求出此时点![]() 的坐标及
的坐标及![]() 的最大值;
的最大值;
(3)如图,动点![]() 以每秒
以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() 出发,沿射线
出发,沿射线![]() 运动;同时,动点
运动;同时,动点![]() 以每秒
以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() 出发,沿射线
出发,沿射线![]() 运动,设运动时间为
运动,设运动时间为![]() (
(![]() ).过
).过![]() 点作
点作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,当点
,当点![]() 、
、![]() 、
、![]() 所组成的三角形是直角三角形时,直接写出
所组成的三角形是直角三角形时,直接写出![]() 的值.
的值.

参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() .
.
【解析】(1)![]() 、
、![]()
∵![]()
∴直线![]() :
:![]()
令![]() 时,
时,![]() ,
,
∴![]()
(点B坐标也可以由二次函数的解析式求得)

(2)连接![]() .∵
.∵![]()
过点![]() 作
作![]() ⊥
⊥![]() 轴交直线
轴交直线![]() 于点
于点![]()
设![]() ,则
,则![]()
![]()
∴![]()
![]()
![]()
∵![]() ,∴
,∴![]() 时
时![]() 有最大值,
有最大值,![]()
此时,![]()
(3)![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国平均每平方千米的土地一年从太阳得到的能量,相当于燃烧130 000 000kg的煤所产生的能量.把130 000 000kg用科学记数法可表示为 kg.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2a-1与a-5是正数m的平方根,则m的值为________.
-
科目: 来源: 题型:
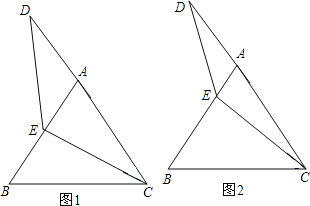
查看答案和解析>>【题目】等边△ABC中,点E在AB上,点D在CA的延长线上,且ED=EC.试探索以下问题:
(1)如图1,当E为AB中点时,试确定线段AD与BE的大小关系,请你直接写出结论:AD BE;
(2)如图2,若点E为线段AB上任意一点,(1)中结论是否成立,若成立,请证明结论,若不成立,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市2016年国庆节这天的最高气温是8℃,最低气温是﹣2℃,则该市这天的最高气温比最低气温高℃.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6,BC=8,则四边形EFGH的面积是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一元二次方程x2-8x-1=0配方得___________________.
相关试题

