【题目】如图,已知A(-4,![]() ),B(-1,2)是一次函数y=kx+b与反比例函数y=
),B(-1,2)是一次函数y=kx+b与反比例函数y=![]() (m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D。
(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D。

(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标。
参考答案:
【答案】(1)、-4<x<-1;(2)、y=![]() ;m=-2;(3)、(
;m=-2;(3)、(![]() ,
,![]() ).
).
【解析】
试题分析:(1)、根据图示直接得出答案;(2)、将A、B两点坐标代入一次函数解析式求出k和b的值,将点B的坐标代入反比例函数解析式求出m的值;(3)、首先根据一次函数设出点P的坐标,求出AC、OC、BD、OD的长度,根据△PCA和△PDB的面积相等列出关于x的方程求出x的值,然后得出点P的坐标.
试题解析:(1)、由图象,当-4<x<-1时,一次函数值大于反比例函数的值
(2)、把A(-4,![]() ),B(-1,2)代入y=kx+b得,
),B(-1,2)代入y=kx+b得, 解得:
解得:![]()
∴ 一次函数的解析式为y=![]()
把B(-1,2)代入y=![]() 得m=-2,即m的值为-2
得m=-2,即m的值为-2
(3)、设P的坐标为(x,![]() ),由A、B的坐标可知AC=
),由A、B的坐标可知AC=![]() ,OC=4,BD=1,OD=2,
,OC=4,BD=1,OD=2,
易知△PCA的高为x+4,△PDB的高2-(![]() ),由
),由![]() 可得
可得
![]() ,解得
,解得![]() ,此时
,此时![]()
∴ P点坐标为(![]() ,
,![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查某市中小学生对“营养午餐”的满意程度,适合采用的调查方式是 . (填“全面调查”或“抽样调查”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数据中,能构成三角形的是( )
A. 1、2、3 B. 2、3、4 C. 4、9、4 D. 2、1、4
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们学校教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:30)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
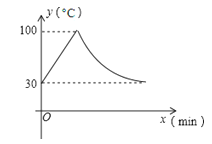
A.7:00 B.7:05 C.7:10 D.7:15
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校举办“迎奥运”知识竞赛,设一、二、三等奖共12名,奖品发放方案如下表:
一等奖
二等奖
三等奖
1盒福娃和1枚徽章
一盒福娃
一枚徽章
用于购买奖品的总费用不少于1000元但不超过1100元,小明在购买“福娃”和徽章前,了解到如下信息:
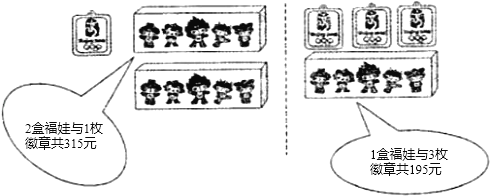
(1)求一盒“福娃”和一枚徽章各多少元?
(2)若本次活动设一等奖2名,则二等奖和三等奖应各设多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形ABCD中,AD∥BC,∠ADC=90°,AD=6,BC=4,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.
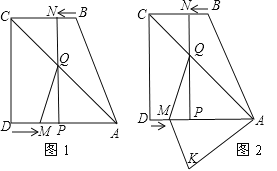
(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值.
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,则AC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级(1)班所有学生参加
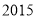 年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为
年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为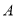 、
、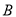 、
、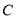 、
、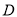 四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题: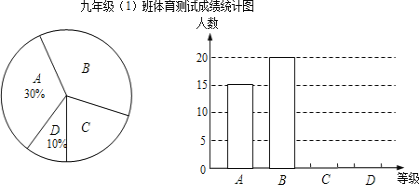
(1)九年级(1)班参加体育测试的学生有 人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,等级
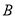 部分所占的百分比是 ,等级
部分所占的百分比是 ,等级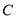 对应的圆心角的度数为 ;
对应的圆心角的度数为 ;(4)若该校九年级学生共有850人参加体育测试,估计达到
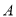 级和
级和 级的学生共有 人.
级的学生共有 人.
相关试题

