【题目】已知一个正多边形的一个外角为36°,则这个正多边形的边数是( )
A.8
B.9
C.10
D.11
参考答案:
【答案】C
【解析】360°÷36°=10,所以这个正多边形是正十边形.
所以答案是:C.
【考点精析】通过灵活运用多边形内角与外角,掌握多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形三个内角的度数之比为2∶3∶5,这个三角形一定是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a3+a2=2a5
B.a3a2=a6
C.a3÷a2=a
D.(a3)2=a9 -
科目: 来源: 题型:
查看答案和解析>>【题目】若x+y=6,x-y=5,则x2-y2等于( )
A. 11B. 15C. 30D. 60
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:ab – a=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(14分)如图1,△ABC是边长为4cm的等边三角形,边AB在射线OM上,且OA=6cm,点D从O点出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连结DE.
(1)求证:△CDE是等边三角形;
(2)如图2,当6<t<10时,△BDE的周长是否存在最小值?若存在,求出△BDE的最小周长;若不存在,请说明理由;
(3)如图3,当点D在射线OM上运动时,是否存在以D、E、B为顶点的三角形是直角三角形?若存在,求出此时t的值;若不存在,请说明理由.
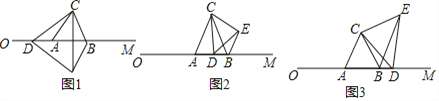
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标.

相关试题

