【题目】如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(6,8),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点E的坐标为 .

参考答案:
【答案】(16,3)或(4![]() +6,2
+6,2![]() ﹣2)或(
﹣2)或(![]() ,
,![]() ).
).
【解析】
试题分析:先依据勾股定理求得OD=10,①当OD=DF时,由勾股定理可求得AF=6,故此可求得OF=12,由翻折的性质可知DC=10,从而得到点E的横坐标为16,FB=4,最后在Rt△EFB中,依据勾股定理列方程求解即可;②当OD=OF时.先求得AF=4,由勾股定理可求得DF=4![]() ,从而得到点E的横坐标为6+4
,从而得到点E的横坐标为6+4![]() ,FB=4
,FB=4![]() ﹣4,最后在Rt△EFB中,依据勾股定理列方程求解即可;③当OF=DF时,设点F的坐标为(b,0),依据两点间的距离公式列出关于b的方程可求得b=
﹣4,最后在Rt△EFB中,依据勾股定理列方程求解即可;③当OF=DF时,设点F的坐标为(b,0),依据两点间的距离公式列出关于b的方程可求得b=![]() .即OF=
.即OF=![]() ,从而得到AF=
,从而得到AF=![]() ,依据勾股定理可求得DF=
,依据勾股定理可求得DF=![]() ,从而得到点E的横坐标为
,从而得到点E的横坐标为![]() ,BF=6,最后在Rt△EFB中,依据勾股定理列方程求解即可.
,BF=6,最后在Rt△EFB中,依据勾股定理列方程求解即可.
解:∵点D的坐标为(6,8),
∴OD=10.
①当OD=DF=10时.
∵DF=10,AD=8,
∴AF=6.
∴OF=12.
由翻折的性质可知:DC=DF=10,FE=CE,
∴点E的横坐标为16.
∴FB=4.
设点E的纵坐标为a,则FE=8﹣a.
在Rt△EFB中,FB2+BE2=FE2,即42+a2=(8﹣a)2,解得a=3.
∴点E的坐标为(16,3).
②当OD=OF时.
∵OF=10,0A=6,
∴AF=4.
∵在Rt△DAF中,DF=![]() =4
=4![]() .
.
∴点E的横坐标为6+4![]() .
.
∴FB=4![]() ﹣4.
﹣4.
设点E的纵坐标为a,则FE=8﹣a.
在Rt△EFB中,FB2+BE2=FE2,即(4![]() ﹣4)2+a2=(8﹣a)2,解得a=2
﹣4)2+a2=(8﹣a)2,解得a=2![]() ﹣2.
﹣2.
∴点E的坐标为(4![]() +6,2
+6,2![]() ﹣2).
﹣2).
③当OF=DF时,设点F的坐标为(b,0),则82+(b﹣6)2=b2.解得:b=![]() .即OF=
.即OF=![]() .
.
∵OA=6,OF=![]() ,
,
∴AF=![]() .
.
∴DF=![]() =
=![]() .
.
由翻折的性质可知:DC=DF,则点E的横坐标为![]() +6=
+6=![]() .
.
在Rt△EFB中,FB2+BE2=FE2,即(![]() ﹣
﹣![]() )2+a2=(8﹣a)2,解得a=
)2+a2=(8﹣a)2,解得a=![]() .
.
∴点E的坐标为(![]() ,
,![]() ).
).
综上所述,点E的坐标为(16,3)或(4![]() +6,2
+6,2![]() ﹣2)或(
﹣2)或(![]() ,
,![]() ).
).
故答案为:(16,3)或(4![]() +6,2
+6,2![]() ﹣2)或(
﹣2)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣4x=12的根是( )
A.x1=2,x2=﹣6 B.x1=﹣2,x2=6 C.x1=﹣2,x2=﹣6 D.x1=2,x2=6
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品进价a元,商店将价格提高30%作零售价销售,在销售旺季过后,商店以8折的价格开展促销活动,这时一件商品的售价为( )
A. a元 B. 1.04a元 C. 0.8a元 D. 0.92a元
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上林老师出示了问题:如图,AD∥BC,∠AEF=90°,AD=AB=BC=DC,∠B=90°,点E是边BC的中点,且EF交∠DCG的平分线CF于点F,求证:AE=EF.
同学们作了一步又一步的研究:
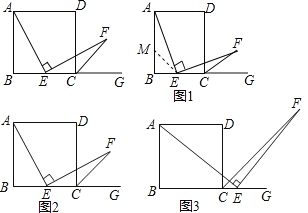
(1)经过思考,小明展示了一种解题思路:如图1,取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF,小明的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小颖提出一个新的想法:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(3)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.

(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值
(1)2b2+(a+b)(ab)(ab)2,其中a=3,b=
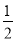
(2)(2a+b)2-(3a-b)2+5a(a-b),其中a=
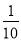 ,b=
,b=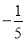
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=3时,代数式px3+qx+1的值为2,则当x=﹣3时,px3+qx+1的值是( )
A. 2 B. 1 C. 0 D. ﹣1
相关试题

