【题目】如图(a),将两块直角三角尺的直角顶点C叠放在一起. 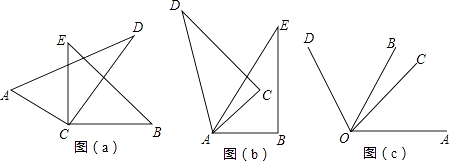
(1)若∠DCE=35°,∠ACB=;若∠ACB=140°,则∠DCE=;
(2)猜想∠ACB与∠DCE的大小有和特殊关系,并说明理由;
(3)如图(b),若是两个同样的三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小有何关系,请说明理由;
(4)已知∠AOB=α,∠COD=β(α,β都是锐角),如图(c),若把它们的顶点O重合在一起,请直接写出∠AOD与∠BOC的大小关系.
参考答案:
【答案】
(1)145°;40°
(2)解:∠ACB+∠DCE=180°,
理由如下:∵∠ACB=∠ACD+∠BCD,
=90°+∠BCD,
∴∠ACB+∠DCE,
=90°+∠BCD+∠DCE,
=90°+∠BCE,
=180
(3)解:∠DAB+∠CAE=120°,
理由如下:
∵∠DAB=∠DAC+∠CAB,
=60°+∠CAB,
∴∠DAB+∠CAE,
=60°+∠CAB+∠CAE,
=60°+∠EAB,
=120°
(4)解:∠AOD+∠BOC=α+β,理由是:
∵∠AOD=∠DOC+∠COA=β+∠COA,
∴∠AOD+∠BOC=β+∠COA+∠BOC,
=β+∠AOB,
=α+β
【解析】解:(1)若∠DCE=35°, ∵∠ACD=90°,∠DCE=35°,
∴∠ACE=90°﹣35°=55°,
∵∠BCE=90°,
∴∠ACB=∠ACE+∠BCE=55°+90°=145°;
若∠ACB=140°,
∵∠BCE=90°,
∴∠ACE=140°﹣90°=50°,
∵∠ACD=90°,
∴∠DCE=90°﹣50°=40°,
所以答案是:145°;40°;
【考点精析】认真审题,首先需要了解余角和补角的特征(互余、互补是指两个角的数量关系,与两个角的位置无关).
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣4y2=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是以x为自变量的二次函数,且当x=0时,y的最小值为-1,写出一个满足上述条件的二次函数表达式_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用图象法求方程的解,体现了数形结合的方法,它是将方程的解看成两个函数图象交点的横坐标.若关于x的方程x2+a﹣
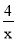 =0(a>0)只有一个整数解,则a的值等于 .
=0(a>0)只有一个整数解,则a的值等于 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在第二象限到x轴距离为2,到y轴距离为5的点的坐标是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系XOY中,A
 ,B
,B ,C
,C .
.(1)请画出
 关于
关于 轴对称的
轴对称的 (其中
(其中 分别是
分别是 的对应点,不写画法);
的对应点,不写画法);(2)直接写出
 三点的坐标:
三点的坐标:  .
.(3)计算△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A、1.5小时以上;B、1~1.5小时;C、0.5~1小时;D、0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
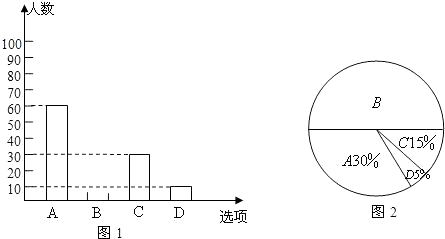
(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.
相关试题

