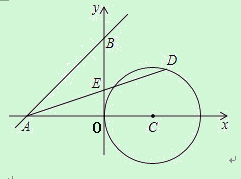
【题目】如图,已知直线y=x+4与两坐标轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是 .
参考答案:
【答案】8﹣2![]() 和8+2
和8+2![]()
【解析】首先由一次函数解析式求出OA、OB的长,而△ABE中,BE边上的高是OA,且OA为定值,所以求△ABE面积的最小值和最大值,转化为求BE的最小值和最大值。过点A作⊙C的两条切线AD、AD′,当动点运动到D点时,BE最小,即△ABE面积最小;当动点运动到D′点时,BE最大,即△ABE面积最大。最后根据比例求出BE 、BE′的值,进而求出△ABE面积的最小值和最大值.
解:由y=x+4得:
当x=0时,y=4,当y=0时,x=﹣4,
∴OA=4,OB=4,
∵△ABE的边BE上的高是OA,
∴△ABE的边BE上的高是4,
∴要使△ABE的面积最大或最小,只要BE取最大值或最小值即可,
过A作⊙C的两条切线,如图,

当动点运动到D点时,BE最小,即△ABE面积最小;
当动点运动到D′点时,BE最大,即△ABE面积最大;
∵x轴⊥y轴,OC为半径,
∴EE′是⊙C切线,
∵AD′是⊙C切线,
∴OE′=E′D′,
设E′O=E′D′=x,
∵AC=4+2=6,CD′=2,AD′是切线,
∴∠AD′C=90°,由勾股定理得:AD′=4![]() ,
,
∴sin∠CAD′=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:x=![]() ,
,
∴BE′=4+![]() ,BE=4﹣
,BE=4﹣![]() ,
,
∴△ABE的最小值是![]() ×(4﹣
×(4﹣![]() )×4=8﹣2
)×4=8﹣2![]() ,
,
最大值是:![]() ×(4+
×(4+![]() )×4=8+2
)×4=8+2![]() ,
,
故答案为:8﹣2![]() 和8+2
和8+2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2-2的顶点坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各情景分别可以用哪一幅图来近似的刻画?正确的顺序是( )
①汽车紧急刹车(速度与时间的关系)
②人的身高变化(身高与年龄的关系)
③跳过运动员跳跃横杆(高度与时间的关系)
④一面冉冉上升的红旗(高度与时间的关系)

A.abcd B.dabc C.dbca D.cabd
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数 y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.其中正确的命题是( )
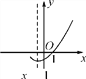
A. ①② B. ②③ C. ①③ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则图中阴影部分的周长为( )
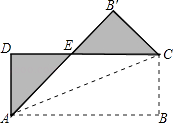
A.16
B.19
C.22
D.25 -
科目: 来源: 题型:
查看答案和解析>>【题目】若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是( )
A.矩形
B.菱形
C.对角线相等的四边形
D.对角线互相垂直的四边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】以下问题,不适合用全面调查的是( )
A.旅客上飞机前的安检
B.学校招聘教师,对应聘人员的面试
C.了解全校学生的课外读书时间
D.了解一批灯泡的使用寿命
相关试题

