【题目】如图，在平面直角坐标系中，抛物线y=-x2+x+3与x轴交于A，B两点（点A在点B左侧），与y轴交于点C：连接BC，点P为线段BC上方抛物线上的一动点，连接OP交BC于点Q．

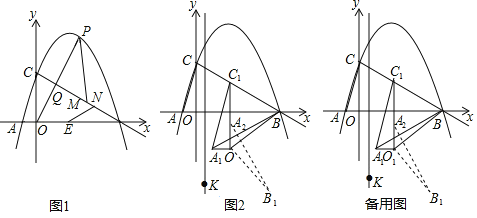
（1）如图1，当值最大时，点E为线段AB上一点，在线段BC上有两动点M，N（M在N上方），且MN=1，求PM+MN+NE-BE的最小值；

（2）如图2，连接AC，将△AOC沿射线CB方向平移，点A，C，O平移后的对应点分别记作A1，C1，O1，当C1B=O1B时，连接A1B、O1B，将△A1O1B绕点O1沿顺时针方向旋转90°后得△A2O1B1在直线x=上是否存在点K，使得△A2B1K为等腰三角形？若存在，直接写出点K的坐标；不存在，请说明理由．

【答案】（1）；（2）K1（，），K2（，-2），K3（，-5），K4（，）

【解析】

（1）先求出抛物线与坐标轴的交点坐标，待定系数法求出直线BC解析式，过P作PT∥y轴交BC于T，构造△PTQ∽△ACQ，设点P的横坐标为m，通过相似三角形性质得出关于m的函数表达式，利用二次函数最值即可；

（2）存在．先求出△AOC沿射线CB方向平移，并能使C1B=O1B时△A1O1B各顶点的坐标，在求出△A1O1B绕点O1沿顺时针方向旋转90°后得△A2O1B1的各顶点坐标，最后按照△A2B1K为等腰三角形进行分类讨论即可．

解：（1）在抛物线y=-x2+x+3中，令x=0，得y=3，∴C（0，3）；

令y=0，得-x2+x+3=0，解得：x1=-1，x2=4，∴B（4，0）

设直线BC解析式为y=kx+b，将B（4，0），C（0，3）；代入并解得：k=，b=3

∴直线BC解析式为y=x+3；

过P作PT∥y轴交BC于T，设P（t，++3），则T（t，+3），如图所示：

∴PT=（++3）-（+3）=+3t，OC=3；

∵PT∥y轴

∴△PTQ∽△ACQ

∴==+t=

∴当t=2时，值最大；此时，P（2，），PT=3；

在Rt△BOC中，BC==5，

∴当NE⊥BC时，NE=BE，此时，NE-BE=0最小，

∵MN=1，∴PM+MN的最小值即PM最小值

∴PM⊥BC时，PM最小

过P作PM⊥BC于M，∴∠PMT=∠BOC=90°

∵∠PTM=∠BCO

∴=

∴PM=PT=，

故PM+MN+NE-BE的最小值=；

（2）存在．在△AOC中，∠AOC=90°，OA=1，OC=3，∴AC=

如图2，

由平移得：C1O1=OC=3，A1O1=OA=1，A1C1=AC=，

∵C1B=O1B，C1O1⊥OB

∴C1G=C1O1=

∴BG=2，OG=2

∴C1（2，），O1（2，），A1（1，）；

∴C1B=O1B=，A1B==；

∵△A1O1B绕点O1沿顺时针方向旋转90°后得△A2O1B1，

∴A2O1=1，O1B1=，A2B1=；

∴A2（2，），B1（，）

∵△A2B1K为等腰三角形，

∴A2K=B1K或A2B1=B1K或A2K=A2B1，

设K（，m）

①当A2K=B1K时，则：+=+，解得：m=-，∴K1（，），

②当A2B1=B1K时，则：+=，解得：m1=-2，m2=-5，∴K2（，-2），K3（，-5），

③当A2K=A2B1时，则：+=，解得：m1=（舍），m2=，∴K4（，）；

综上所述，点K的坐标为：K1（，），K2（，-2），K3（，-5），K4（，）．

关闭