【题目】计算(x﹣1)(﹣x﹣1)的结果是( )
A.﹣x2+1
B.x2﹣1
C.﹣x2﹣1
D.x2+1
参考答案:
【答案】A
【解析】解:(x﹣1)(﹣x﹣1)=﹣(x﹣1)(x+1)=﹣x2+1. 故选A.
【考点精析】掌握平方差公式是解答本题的根本,需要知道两数和乘两数差,等于两数平方差.积化和差变两项,完全平方不是它.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算: 3a-2a= ▲ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.

(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案:
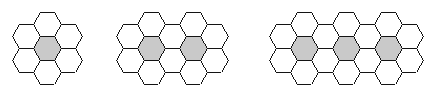
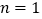
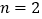

⑴ 当黑砖n=1时,白砖有_______块,当黑砖n=2时,白砖有________块,
当黑砖n=3时,白砖有_______块.
⑵ 第n个图案中,白色地砖共 块.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的直径是10,圆心O到直线l的距离是5,则直线l和⊙O的位置关系是( )
A.相离
B.相交
C.相切
D.外切 -
科目: 来源: 题型:
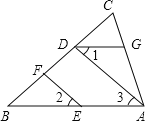
查看答案和解析>>【题目】按图填空,并注明理由.
⑴完成正确的证明:如图,已知AB∥CD,求证:∠BED=∠B+∠D
证明:过E点作EF∥AB(经过直线外一点有且只有一条直线与这条直线平行)
∴∠1= ( )
∵AB∥CD(已知)
∴EF∥CD(如果两条直线与同一直线平行,那么它们也平行)
∴∠2= ( )
又∠BED=∠1+∠2
∴∠BED=∠B+∠D (等量代换).
⑵如图,在△ABC中,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解:因为EF∥AD(已知)
所以∠2=∠3.( )
又因为∠1=∠2,所以∠1=∠3.(等量代换)
所以AB∥ ( )
所以∠BAC+ =180°( ).
又因为∠BAC=70°,所以∠AGD=110°.

图⑴ 图⑵
-
科目: 来源: 题型:
查看答案和解析>>【题目】同一时刻,同一地区,太阳光下物体的高度与投影长的比是________.
相关试题

