搜索
【题目】如图所示，在长为a米，宽为b米的长方形地面上修两条同样宽的道路，余下的部分作为绿化地，路宽为x米．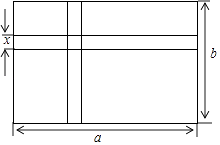 
（1）用代数式表示绿化地的面积．
（2）若a=63，b=43，x=3，绿化地每平方米为15元，道路每平方米150元，计算该工程需花费多少元？
参考答案：
【答案】
（1）解：绿化地的面积是（a﹣x）（b﹣x）m2
（2）解：∵a=63，b=43，x=3，绿化地每平方米为15元，道路每平方米150元，
∴该工程需花费的钱数为：15（a﹣x）（b﹣x）+150（ax+bx+x2）
=15×（63﹣3）×（43﹣3）+150×（63×3+43×3+9）
=82050（元）
【解析】（1）根据图形列出算式即可；（2）先列出算式，再代入求出即可．
【考点精析】掌握代数式求值是解答本题的根本，需要知道求代数式的值，一般是先将代数式化简，然后再将字母的取值代入；求代数式的值，有时求不出其字母的值，需要利用技巧，“整体”代入．
-
科目： 来源： 题型：
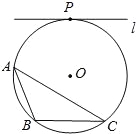
查看答案和解析>>【题目】如图，⊙O为△ABC的外接圆，直线l与⊙O相切与点P，且l∥BC．
（1）请仅用无刻度的直尺，在⊙O中画出一条弦，使这条弦将△ABC分成面积相等的两部分（保留作图痕迹，不写作法）；
（2）请写出证明△ABC被所作弦分成的两部分面积相等的思路．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列各近似数精确到万位的是（ ）
A.35000
B.4亿5千万
C.8.9×104
D.4×104 -
科目： 来源： 题型：
查看答案和解析>>【题目】问题提出：用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？
问题探究：不妨假设能搭成
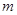种不同的等腰三角形，为探究
之间的关系，我们可以从特殊入手，通过试验、观察、类比，最后归纳、猜测得出结论．探究一：
（1）用3根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
此时，显然能搭成一种等腰三角形。所以，当
时，
（2）用4根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
只可分成1根木棒、1根木棒和2根木棒这一种情况，不能搭成三角形
所以，当
时，
（3）用5根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
若分成1根木棒、1根木棒和3根木棒，则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒，则能搭成一种等腰三角形
所以，当
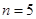时，（4）用6根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
若分成1根木棒、1根木棒和4根木棒，则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒，则能搭成一种等腰三角形
所以，当
时，综上所述，可得表①
3
4]
5
6
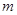
1
0
1
1
探究二：
（1）用7根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三角形？
（仿照上述探究方法，写出解答过程，并把结果填在表②中）
（2）分别用8根、9根、10根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三
角形？（只需把结果填在表②中）
7
8
9
10
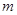
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究，……
解决问题：用
根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？（设
分别等于
、
、
、
，其中
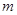
是整数，把结果填在表③中）问题应用：用2016根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？（要求写出解答过程）其中面积最大的等腰三角形每个腰用了__________________根木棒。（只填结果）
-
科目： 来源： 题型：
查看答案和解析>>【题目】在每个小正方形的边长为1的网格中,点A,B,C,D均在格点上,点E,F分别为线段BC,DB上的动点,且BE=DF.
(1)如图①所示,当BE=
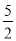时,计算AE+AF的值等于____;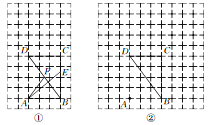
(2)当AE+AF取最小值时,请在如图②所示的网格中,用无刻度的直尺,画出线段AE,AF,并简要说明点E和点F的位置是如何找到的(不要求证明)
-
科目： 来源： 题型：
查看答案和解析>>【题目】等腰三角形一边长等于5，一边长等于9，则它的周长是( )
A. 14 B. 23 C. 19 D. 19或23
-
科目： 来源： 题型：
查看答案和解析>>【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
相关试题
