Question

【题目】如图，将正方形 OABC 放在平面直角坐标系中，O 是原点，A 的坐标为(1，)，则点C 的坐标为（ ）

A. (﹣1，) B. (，1) C. ( ，3) D. ( ，2)

Answer 1

【答案】B

【解析】

过点A作AD⊥x轴于D，过点C作CE⊥x轴于E，根据同角的余角相等求出∠OAD=∠COE，再利用“角角边”证明△AOD和△OCE全等，根据全等三角形对应边相等可得OE=AD，CE=OD，然后根据点C在第二象限写出坐标即可．

如图，过点A作AD⊥x轴于D，过点C作CE⊥x轴于E，

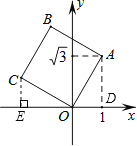
∵四边形OABC是正方形，
∴OA=OC，∠AOC=90°，
∴∠COE+∠AOD=90°，
又∵∠OAD+∠AOD=90°，
∴∠OAD=∠COE，
在△AOD和△OCE中，

，
∴△AOD≌△OCE（AAS），
∴OE=AD=，CE=OD=1，
∵点C在第二象限，
∴点C的坐标为（-，1）．
故选：B．