【题目】如图,正方形ABCD与正方形AEFG起始时互相重合,现将正方形AEFG绕点A逆时针旋转,设旋转角∠BAE=α(0°<α<360°),则当正方形的顶点F落在正方形的对角线AC或BD所在直线上时,α= . 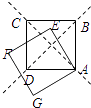
参考答案:
【答案】60°或180°
【解析】解:依照题意画出图形,如图所示. 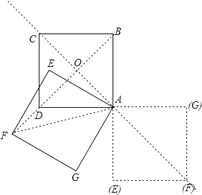
①当点F在BD上时:令AC、BD的交点为O,设正方形ABCD的边长为2a,
则AC=AF=2 ![]() a,AO=
a,AO= ![]() AC=
AC= ![]() a.
a.
∵四边形ABCD为正方形,
∴AC⊥BD,∠BAC=∠DAC=∠EAF=45°,
∴∠AOF=90°.
在Rt△AOF中,AO= ![]() a,AF=2
a,AF=2 ![]() a,
a,
∴cos∠OAF= ![]() =
= ![]() ,
,
∴∠OAF=60°,∠OAE=∠OAF﹣∠EAF=15°,
∴α=∠BAE=∠BAC+∠OAE=60°;
②当点F在AC上时,
∵C、A、F三点共线,∠EAF=∠BAC=45°,
∴B、A、E三点共线,
∴α=∠BAE=180°.
综上可知:当正方形的顶点F落在正方形的对角线AC或BD所在直线上时,α=60°或180°.
所以答案是:60°或180°.
【考点精析】本题主要考查了正方形的性质和旋转的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.
-
科目: 来源: 题型:
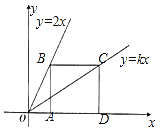
查看答案和解析>>【题目】如图,点B、C分别在直线y=2x和y=kx上,点A、D是x轴上的两点,且四边形ABCD是正方形.
(1)若正方形ABCD的边长为2,则点B、C的坐标分别为 .
(2)若正方形ABCD的边长为a,求k的值.
-
科目: 来源: 题型:
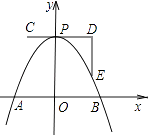
查看答案和解析>>【题目】如图,一条抛物线与x轴相交于A,B两点,其顶点P在折线C﹣D﹣E上移动,若点C,D,E的坐标分别为(﹣1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
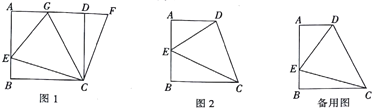
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E是AB上一点,点F是AD延长线上一点,且DF=BE,连接CE、CF.
(1)求证:CE=CF.
(2)在图1中,若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
(3)根据你所学的知识,运用(1)、(2)解答中积累的经验,完成下列各题,如图2,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,且∠DCE=45°.
①若AE=6,DE=10,求AB的长;
②若AB=BC=9,BE=3,求DE的长.
-
科目: 来源: 题型:
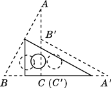
查看答案和解析>>【题目】如图,直角三角板ABC的斜边AB=12 cm,∠A=30°,将三角板ABC绕点C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为( )
A. 6 cm B. 4 cm
C. (6-2
 )cm D. (4
)cm D. (4 -6)cm
-6)cm -
科目: 来源: 题型:
查看答案和解析>>【题目】根据题意解答
(1)解不等式组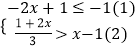
(2)如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,若∠CBF=20°,求∠ADE的度数.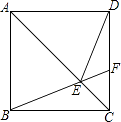
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形ABCD对折,得折痕PQ,展开后再沿MN翻折,使点C恰好落在折痕PQ上的点C′处,点D落在D′处,其中M是BC的中点且MN与折痕PQ交于F.连接AC′,BC′,则图中共有等腰三角形的个数是( )
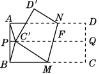
A. 1 B. 2 C. 3 D. 4
相关试题

