搜索
【题目】四边形ABCD中，对角线AC、BD交于点O，给出下列四组条件：①AB∥CD，AD∥BC；②AB∥CD，∠A＝∠C；③AO＝CO，BO＝DO；④AB∥CD，AD＝BC．
一定能判定四边形ABCD是平行四边形的条件有----------------------------（ ）
A. 1组 B. 2组 C. 3组 D. 4组
参考答案：
【答案】C
【解析】如图，（1）∵AB∥CD，AD∥BC，
∴四边形ABCD是平行四边形；
（2）∵AB∥CD，
∴∠ABC+∠BCD=180°，
又∵∠BAD=∠BCD，
∴∠BAD+∠ABC=180°，
∴AD∥BC，
∴四边形ABCD是平行四边形；
（3）∵在四边形ABCD中，AO＝CO，BO＝DO，
∴四边形ABCD是平行四边形；
（4）∵在四边形ABCD中，AB∥CD，AD＝BC，
∴四边形ABCD可能是等腰梯形，也可能是平行四边形；
综上所述，上述四组条件一定能判定四边形ABCD是平行四边形的有3组.
故选C.
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了解某市市民“绿色出行”方式的情况，某校数学兴趣小组以问卷调查的形式，随机调查了某市部分出行市民的主要出行方式（参与问卷调查的市民都只从以下五个种类中选择一类），并将调查结果绘制成如下不完整的统计图．
种类
A
B
C
D
E
出行方式
共享单车
步行
公交车
的士
私家车
根据以上信息，回答下列问题：
（1）参与本次问卷调查的市民共有 人，其中选择B类的人数有 人；
（2）在扇形统计图中，求A类对应扇形圆心角α的度数，并补全条形统计图；
（3）该市约有12万人出行，若将A，B，C这三类出行方式均视为“绿色出行”方式，请估计该市“绿色出行”方式的人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某旅游团上午6时从旅馆出发，乘汽车到距离210km的某著名旅游景点游玩，该汽车离旅馆的距离S（km）与时间t（h）的关系可以用如图的折线表示．根据图象提供的有关信息，解答下列问题：
（1）求该团去景点时的平均速度是多少？
（2）该团在旅游景点游玩了多少小时？
（3）求返回到宾馆的时刻是几时几分？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
ABCD中，∠DAB＝60°，点E，F分别在CD，AB的延长线上，且AE＝AD，CF＝CB． 
（1）求证：四边形AFCE是平行四边形．
（2）若去掉已知条件的“∠DAB＝60°，上述的结论还成立吗 ”若成立，请写出证明过程；若不成立，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在矩形ABCD中，AB=3，将△ABD沿对角线BD对折，得到△EBD，DE与BC交于点 F，∠ADB=30°，则EF=---------------------------------------------（ ）
A. 3
B. 2 C. 3 D. -
科目： 来源： 题型：
查看答案和解析>>【题目】本市新建一座圆形人工湖，为测量该湖的半径，小杰和小丽沿湖边选取A，B，C三根木柱，使得A，B之间的距离与A，C之间的距离相等，并测得BC长为120米，A到BC的距离为4米，如图所示．
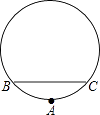
（1）请你帮他们求出该湖的半径；
（2）如果在圆周上再另取一点P，建造一座连接B，C，P三点的三角形艺术桥，且△BCP为直角三角形，问：这样的P点可以有几处？如何找到？ -
科目： 来源： 题型：
查看答案和解析>>【题目】在一次期中考试中，
（1）一个班级有甲、乙、丙三名学生，分别得到70分、80分、90分．这三名同学的平均得分是多少？
（2）一个班级共有40名学生，其中5人得到70分，20人得到80分，15人得到90分．求班级的平均得分．
（3）一个班级中，20%的学生得到70分，50%的学生得到80分，30%的学生得到90分．求班级的平均得分．
（4）中考的各学科的分值依次为：数学150分，语文150分，物理100分，政治50分，历史50分，合计总分为500分． 在这次期中考试中，各门学科的总分都设置为100分，现已知甲、乙两名学生的得分如下表：学科
数学
语文
物理
政治
历史
甲
80
90
80
80
70
乙
80
80
70
80
95
你认为哪名同学的成绩更理想，写出你的理由．
相关试题
