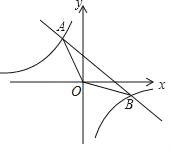
【题目】如图,O为坐标原点,点A(﹣1,5)和点B(m,﹣1)均在反比例函数![]() 图象上
图象上
(1)求m,k的值;
(2)当x满足什么条件时,﹣x+4>﹣![]() ;
;
(3)P为y轴上一点,若△ABP的面积是△ABO面积的2倍,直接写出点P的坐标.
参考答案:
【答案】(1) k=﹣5,m=5;(2) x<﹣1或0<x<5时,﹣x+4>﹣![]() ;(3) P(0,12)或(0,﹣4).
;(3) P(0,12)或(0,﹣4).
【解析】
(1)利用待定系数法即可解决问题;
(2)观察图象直线y=﹣x+4的图象在反比例函数y=![]() 的图象的上方时,对应的自变量的取值范围就是不等式的解集;
的图象的上方时,对应的自变量的取值范围就是不等式的解集;
(3)构建方程即可解决问题;
(1)点A(﹣1,5)和点B(m,1)均在反比例函数![]() 图象上,
图象上,
∴k=﹣5,m=5;
(2)∵A(﹣1,5),B(5,﹣1)是直线y=﹣x+4与反比例函数y=![]() 的交点,
的交点,
观察图象可知:x<﹣1或0<x<5时,﹣x+4>﹣![]() ;
;
(3)设P(0,m),
∵直线AB交y轴于(0,4),
∴![]() ×|m﹣4|×6=2×
×|m﹣4|×6=2×![]() ×4×6,
×4×6,
解得m=12或﹣4,
∴P(0,12)或(0,﹣4);
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为
 ,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
,连接AC、BD交于点O,CE平分∠ACD交BD于点E,(1)求DE的长;
(2)过点EF作EF⊥CE,交AB于点F,求BF的长;
(3)过点E作EG⊥CE,交CD于点G,求DG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】经过某路口的行人,可能直行,也可能左拐或右拐.假设这三种可能性相同,现有两人经过该路口,求下列事件的概率:
(1)“两人都左拐”的概率是 ;恰好有一人直行,另一人左拐的概率是 ;
(2)利用列表法或树状图求出“至少有一人直行”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们都知道连接多边形任意不相邻的两点的线段成为多边形的对角线,也都知道四边形的对角线有2条,五边形的对角线有5条
(1)六边形的对角线有 条,七边形的对角线有 条;
(2)多边形的对角线可以共有20条吗?如果可以,求出多边形的边数,如果不可以,请说明理由.
-
科目: 来源: 题型:
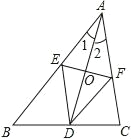
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,线段AD的垂直平分线分别交AB和AC于点E、F,连接DE、DF.
(1)试判定四边形AEDF的形状,并证明你的结论.
(2)若AE=5,AD=8,求EF的长.
(3)△ABC满足什么条件时,四边形AEDF是正方形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC是边长为8的等边三角形,AD⊥BC下点D,DE⊥AB于点E
(1)求证:AE=3EB;
(2)若点F是AD的中点,点P是BC边上的动点,连接PE,PF,如图2所示,求PE+PF的最小值及此时BP的长;
(3)在(2)的条件下,连接EF,若AD=
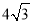 ,当PE+PF取最小值时,△PEF的面积是 .
,当PE+PF取最小值时,△PEF的面积是 .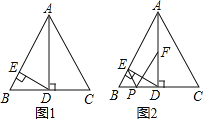
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx﹣3过点A(﹣1,0),B(3,0),点M、N为抛物线上的动点,过点M作MD∥y轴,交直线BC于点D,交x轴于点E.过点N作NF⊥x轴,垂足为点F
(1)求二次函数y=ax2+bx﹣3的表达式;
(2)若M点是抛物线上对称轴右侧的点,且四边形MNFE为正方形,求该正方形的面积;
(3)若M点是抛物线上对称轴左侧的点,且∠DMN=90°,MD=MN,请直接写出点M的横坐标.
相关试题

