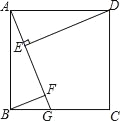
【题目】如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
(1)如图1,求证:AE=BF;
(2)连接DF,若tan∠BAG=![]() ,AB=2
,AB=2![]() ,求△ADF的面积.
,求△ADF的面积.
参考答案:
【答案】(1)见解析;(2)8.
【解析】
(1)利用正方形的性质证明△BAF和△ADE全等.(2)利用(1)和已知条件,分别求出DE,AF长就可以求出三角形面积,
(1)∵四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE,
∴∠AB=AD,∠BAD=90°,∠AED=90°,∠AED=∠BFA,
∴∠BAF+∠EAD=90°,∠EAD+∠ADE=90°,
∴∠BAF=∠ADE,
在△BAF和△ADE中,
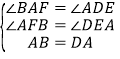 ,
,
∴△BAF≌△ADE(AAS),
∴BF=AE,
即AE=BF;
(2)由(1)知∠AED=∠BFA=90°,
∵tan∠BAG=![]() ,AB=2
,AB=2![]() ,
,
∴tan∠BAF=![]() ,
,
∴AF=4,BF=2,
由(1)知,△BAF≌△ADE,
∴AF=DE,
∴DE=4,
∵∠AED=90°,
∴△ADF的面积是:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,按以下步骤作图:分别以B,C为圆心,以大于
 BC的长为半径作弧,弧线两两交于M、N两点,作直线MN,与边AC、BC分别交于D、E两点,连接BD、AE,若∠BAC=90°,在下列说法中:
BC的长为半径作弧,弧线两两交于M、N两点,作直线MN,与边AC、BC分别交于D、E两点,连接BD、AE,若∠BAC=90°,在下列说法中:
①E为△ABC外接圆的圆心;
②图中有4个等腰三角形;
③△ABE是等边三角形;
④当∠C=30°时,BD垂直且平分AE.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形ABOC是正方形,点A的坐标为(1,1),
 是以点B为圆心,BA为半径的圆弧;
是以点B为圆心,BA为半径的圆弧; 是以点O为圆心,OA1为半径的圆弧,
是以点O为圆心,OA1为半径的圆弧, 是以点C为圆心,CA2为半径的圆弧,
是以点C为圆心,CA2为半径的圆弧, 是以点A为圆心,AA3为半径的圆弧,继续以点B、O、C、A为圆心按上述作法得到的曲线AA1A2A3A4A5…称为正方形的“渐开线”,那么点A5的坐标是______,点A2018的坐标是______.
是以点A为圆心,AA3为半径的圆弧,继续以点B、O、C、A为圆心按上述作法得到的曲线AA1A2A3A4A5…称为正方形的“渐开线”,那么点A5的坐标是______,点A2018的坐标是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(1,a)是反比例函数
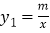 的图象上一点,直线
的图象上一点,直线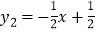 与反比例函数
与反比例函数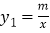 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
(3)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC=______度;
(2)求∠EDF的度数.

-
科目: 来源: 题型:
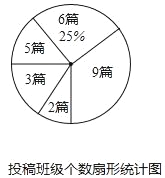
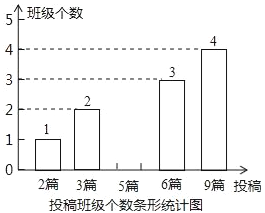
查看答案和解析>>【题目】为积极响应市委,市政府提出的“实现伟大中国梦,建设美丽鄂尔多斯”的号召,康巴什区某校在八,九年级开展征文活动,校学生会对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图.
(1)扇形统计图中投稿篇数为3所对应的扇形的圆心角的度数是_____;该校八,九年级各班在这一周内投稿的平均篇数是______;并将该条形统计图补充完整.
(2)如果要求该校八、九年级的投稿班级个数为30个,估计投稿篇数为5篇的班级个数.
(3)在投稿篇数为9篇的4个班级中,八,九年级各有两个班,校学生会准备从这四个班级中选出两个班参加全市的表彰会,请你用列表法或画树状图的方法求出所选两个班正好不在同一年级的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE的延长线于点D,使得DB=DE.
(1)求证:BD是⊙O的切线;
(2)若AB=12,DB=5,求△AOB的面积.

相关试题

