【题目】已知△ABC是边长为4的等边三角形，BC在x轴上，点D为BC的中点，点A在第一象限内，AB与y轴的正半轴交与点E，已知点B（﹣1，0）．

（1）点A的坐标：　　　　　　，点E的坐标：　　　　　　；

（2）若二次函数y=﹣x2+bx+c过点A、E，求此二次函数的解析式；

（3）P是线段AC上的一个动点（P与点A、C不重合）连结PB、PD，设L是△PBD的周长，当L取最小值时。

求：①点P的坐标

②判断此时点P是否在（2）中所求的抛物线上，请充分说明你的判断理由．

参考答案：

【答案】（1）E（0， ）；（2）y=﹣x2+x+；（3）①P（， ），②此时点P在抛物线上．

【解析】试题分析：

（1）由已知条件求得线段OD、AD、OE的长可得点A、E的坐标；

（2）把（1）中所求得的A、E坐标代入中列方程组求得的值可得抛物线的解析式；

（3）由△PBD中，BD边是定值可知当PB+PD最小时，△PBD的周长最小，因此作点D关于AC的对称点D’，连接BD’，交AC于点P，此时，△PBD的周长最小.①作D’G⊥轴，连接DD’交AC于点F，利用轴对称和等边三角形的性质求得DG、D’G的长可得D’的坐标，用待定系数法求得直线DD’和AC的解析式就可求得点P的坐标；②把所求得的点P的坐标代入（2）中所得抛物线的解析式可判断点P是否在该抛物线上.

试题解析：

（1）连接AD，如图1，

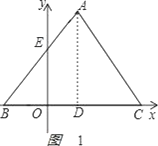
∵△ABC是边长为4的等边三角形，又B的坐标为（﹣1，0），BC在x轴上，A在第一象限，

∴点C在x轴的正半轴上，

∴C的坐标为（3，0），由中点坐标公式，得：D的坐标为（1，0）．

∵D为BC的中点，AB=AC=BC=4，

∴AD⊥BC，

∴AD=，

∴A的坐标是（1， ）．

∵在△BOE中，∠BOE=90°，∠EBO=60°，

∴∠BEO=30°，

∴BE=2BO=2，

∴OE=，

∴点E的坐标为（0， ）；

（2）∵抛物线过点A、E，

∴ ，解得： ， ，

∴抛物线的解析式为；

（3）作点D关于AC的对称点D'，

连接BD'交AC于点P，则PB与PD的和取最小值，

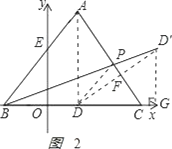
即△PBD的周长L取最小值，如图2．

①∵D、D′关于直线AC对称，

∴DD′⊥AC，∴∠DFC=90°，∵∠ACD=60°，∴∠D′DC=30°，

∴在Rt△DFC中，DF= =，∴DD'=，

作D’G⊥轴于点G，

在Rt△D’DG中，DG=D’Dcos30°=3，DG=D’Dsin30°=，

∴点D'的坐标为（4， ），

∴由待定系数法可求得：直线BD'的解析式为： ，直线AC的解析式为： ，

由 解得： ，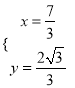

∴点P的坐标．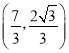

②∵在中，当时， ，

∴点P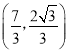在抛物线上.

关闭