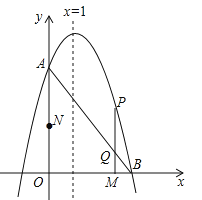
【题目】如图,已知抛物线![]() 与y轴相交于点A(0,3),与x正半轴相交于点B,对称轴是直线x=1.
与y轴相交于点A(0,3),与x正半轴相交于点B,对称轴是直线x=1.
(1)求此抛物线的解析式以及点B的坐标.
(2)动点M从点O出发,以每秒2个单位长度的速度沿x轴正方向运动,同时动点N从点O出发,以每秒3个单位长度的速度沿y轴正方向运动,当N点到达A点时,M、N同时停止运动.过动点M作x轴的垂线交线段AB于点Q,交抛物线于点P,设运动的时间为t秒.
①当t为何值时,四边形OMPN为矩形.
②当t>0时,△BOQ能否为等腰三角形?若能,求出t的值;若不能,请说明理由.
参考答案:
【答案】(1)![]() ,B点坐标为(3,0);(2)①;②.
,B点坐标为(3,0);(2)①;②.
【解析】
试题分析:(1)由对称轴公式可求得b,由A点坐标可求得c,则可求得抛物线解析式;再令y=0可求得B点坐标;
(2)①用t可表示出ON和OM,则可表示出P点坐标,即可表示出PM的长,由矩形的性质可得ON=PM,可得到关于t的方程,可求得t的值;②由题意可知OB=OA,故当△BOQ为等腰三角形时,只能有OB=BQ或OQ=BQ,用t可表示出Q点的坐标,则可表示出OQ和BQ的长,分别得到关于t的方程,可求得t的值.
试题解析:
(1)∵抛物线![]() 对称轴是直线x=1,∴﹣
对称轴是直线x=1,∴﹣![]() =1,解得b=2,∵抛物线过A(0,3),∴c=3,∴抛物线解析式为
=1,解得b=2,∵抛物线过A(0,3),∴c=3,∴抛物线解析式为![]() ,令y=0可得
,令y=0可得![]() ,解得x=﹣1或x=3,∴B点坐标为(3,0);
,解得x=﹣1或x=3,∴B点坐标为(3,0);
(2)①由题意可知ON=3t,OM=2t,∵P在抛物线上,∴P(2t,![]() ),∵四边形OMPN为矩形,∴ON=PM,∴3t=
),∵四边形OMPN为矩形,∴ON=PM,∴3t=![]() ,解得t=1或t=﹣
,解得t=1或t=﹣![]() (舍去),∴当t的值为1时,四边形OMPN为矩形;
(舍去),∴当t的值为1时,四边形OMPN为矩形;
②∵A(0,3),B(3,0),∴OA=OB=3,且可求得直线AB解析式为y=﹣x+3,∴当t>0时,OQ≠OB,∴当△BOQ为等腰三角形时,有OB=QB或OQ=BQ两种情况,由题意可知OM=2t,∴Q(2t,﹣2t+3),∴OQ=![]() =
=![]() ,BQ=
,BQ=![]() =
=![]() |2t﹣3|,又由题意可知0<t<1,当OB=QB时,则有
|2t﹣3|,又由题意可知0<t<1,当OB=QB时,则有![]() |2t﹣3|=3,解得t=
|2t﹣3|=3,解得t=![]() (舍去)或t=
(舍去)或t=![]() ;
;
当OQ=BQ时,则有![]() =
=![]() |2t﹣3|,解得t=
|2t﹣3|,解得t=![]() ;
;
综上可知当t的值为![]() 或
或![]() 时,△BOQ为等腰三角形.
时,△BOQ为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直角三角形中30°角所对的直角边为4cm,则斜边的长为__________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段(单位:cm)能组成三角形的是( )
A. 1,2,1B. 4,5,9C. 6,8,13D. 2,2,4
-
科目: 来源: 题型:
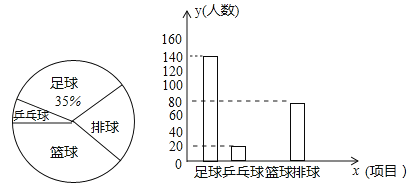
查看答案和解析>>【题目】某校为提高学生身体素质,决定开展足球、篮球、台球、乒乓球四项课外体育活动,并要求学生必须并且只能选择一项.为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并绘制出以下两幅不完整的统计图.请根据统计图回答下列问题.(要求写出简要的解答过程)
(1)这次活动一共调查了多少名学生?
(2)补全条形统计图.
(3)若该学校总人数是1300人,请估计选择篮球项目的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知3m=8,3n=2,则3m+n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的三个内角度数比为1:2:3,则三个外角的度数比为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b=﹣3,ab=1,求a2+b2=_____.
相关试题

