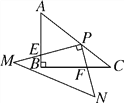
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4.Rt△MPN中,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=________.
参考答案:
【答案】3
【解析】如图作PQ⊥AB于Q,PR⊥BC于R.
∵∠PQB=∠QBR=∠BRP=90°,
∴四边形PQBR是矩形,
∴∠QPR=90°=∠MPN,
∴∠QPE=∠RPF,
∴△QPE∽△RPF,则![]() =
=![]() =2,
=2,
∴PQ=2PR=2BQ.
在Rt△ABC中,AB=3,BC=4,则AC=5.
又∵PQ∥BC,
∴AQ:QP:AP=AB:BC:AC=3:4:5,
设PQ=4x,则AQ=3x,AP=5x,BQ=2x,
∴AQ+BQ=2x+3x=3,得x=![]() ,
,
∴AP=5x=3.
故答案为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】假设我市出租车收费标准是:起步价6元,可乘3千米;3千米到5千米,每千米1.6元;超过5千米,每千米2.4元.
(1)若某人乘坐的路程为4千米,那么他支付的费用是多少?
(2)若某人乘坐了x(x>5)千米的路程,则他应支付的费用是多少?
(3)若某人乘坐的路程为10千米,那么他应支付的费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)
(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)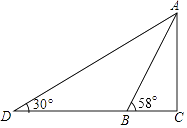
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由6个正方形拼成的一个长方形,如果最小的正方形的边长为1
(Ⅰ)能否求出拼成的长方形的面积?____(填“能”或“不能”);
(Ⅱ)若能,请你写出拼成的长方形的面积;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?

-
科目: 来源: 题型:
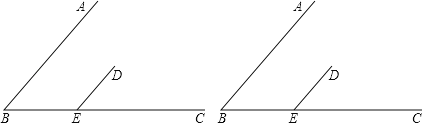
查看答案和解析>>【题目】如图,点D是∠ABC内部一点,DE∥AB交BC于点E.请你画出射线DF,并且DF∥BC;判断∠B与∠EDF的数量关系,并证明.
-
科目: 来源: 题型:
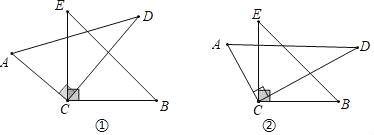
查看答案和解析>>【题目】将一副分别含有30°和45°角的两个三角板的直角顶点C叠放在一起.
①如图,CD平分∠ECB,求∠ACB与∠DCE的和.
②如图,若CD不平分∠ECB,请你直接写出∠ACB与∠DCE之间所具有的数量关系(不要求说出理由).
相关试题

