搜索
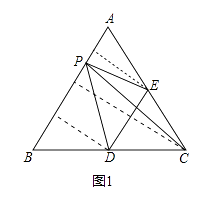
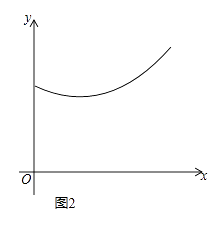
【题目】如图1，在等边△ABC中，点D，E分别是BC，AC边上的中点，点P为AB边上的一个动点，设AP=x，连接PE，PD，PC，DE，其中某条线段的长为y，若表示y与x的函数关系的图象大致如图2所示，则这条线段可能是（ ）
A.线段PE
B.线段PD
C.线段PC
D.线段DE
参考答案：
【答案】A
【解析】解：设等边三角形边长为1，则0≤x≤1，
如图1，分别过点E、C、D作AB的垂线，垂足分别为F、G、H，
根据等边三角形的性质可知，
当x= 
时，线段PE有最小值；
当x= 
时，线段PC有最小值；
当x= 
时，线段PD有最小值；
∵点E、D分别是AC，BC边的中点
∴线段DE的长为定值 ．
根据图2可知，当x= 时，函数有最小值，故这条线段为PE．
所以答案是：A．
【考点精析】解答此题的关键在于理解函数的图象的相关知识，掌握函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
，
，AE平分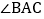
，
，交AC延长线于F，且垂足为E，则下列结论：
；
；
，
；
其中正确的结论有______
填写序号
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
是等腰三角形，
，
．
尺规作图：作
的角平分线BD，交AC于点
保留作图痕迹，不写作法
；
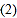判断
是否为等腰三角形，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知∠AOB=70°，∠AOD=
∠AOC，∠BOD=3∠BOC（∠BOC＜45°），则∠BOC的度数是______． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C＝90°，将△ACE沿着AE折叠以后C点正好落在AB边上的点D处．
（1）当∠B＝28°时，求∠AEC的度数；
（2）当AC＝6，AB＝10时，
①求线段BC的长；
②求线段DE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】(10分)如图，在直角坐标系xOy中，A(﹣1，0)，B(3，0)，将A，B同时分别向上平移2个单位，再向右平移1个单位，得到的对应点分别为D，C，连接AD，BC.
(1)直接写出点C，D的坐标：C ，D ；
(2)四边形ABCD的面积为 ；
(3)点P为线段BC上一动点(不含端点)，连接PD，PO.求证：∠CDP+∠BOP=∠OPD.
-
科目： 来源： 题型：
查看答案和解析>>【题目】
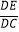如图，点P是菱形ABCD的对角线BD上的一动点，连接CP并延长交AD于E，交BA的延长线于点F．
（1）求证：△APD≌△CPD．
（2）当菱形ABCD变为正方形，且PC=2，tan∠PFA=
时，求正方形ABCD的边长．
相关试题
